题目内容
【题目】如图，在四边形ABCD中，AB∥CD，且AB＝2CD，E，F分别是AB，BC的中点，EF与BD交于点H．
（1）求证：四边形DEBC是平行四边形；
（2）若BD＝6，求DH的长．
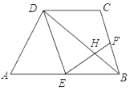
【答案】（1）见解析；（2）DH＝4．
【解析】
（1）由AB=2CD，E是AB的中点得出DC=BE，再结合AB∥CD即可得证；
（2）先证△EDM∽△FBM得
，由BC=DE，F为BC的中点得出=2，继而知DH=2HB，结合DH+HB=6可得答案．
（1）∵E是AB的中点，
∴AB＝2EB，
∵AB＝2CD，
∴DC＝BE，
又∵AB∥CD，即DC∥BE，
∴四边形BCDE是平行四边形．
（2）∵四边形BCDE是平行四边形，
∴BC＝DE，BC∥DE，
∴△EDM∽△FBM，
∴，
∵BC＝DE，F为BC的中点，
∴BF＝
BC＝DE，
∴＝2，
∴DH＝2HB，
又∵DH+HB＝6，
∴DH＝4．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
