Question

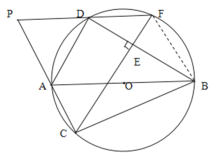
【题目】如图，已知O是Rt△ABC的外接圆，点D是O上的一个动点，且C，D位于AB的两侧，联结AD，BD，过点C作CE⊥BD，垂足为E。延长CE交O于点F，CA，FD的延长线交于点P。

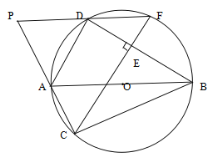
求证：（1）弧AF=弧DC;

（2）△PAD是等腰三角形.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

(1)连接BF，根据在同圆中，同弧所对的圆周角相等，可得∠CAB=∠CFB；再根据直径所对的圆周角为直角，逐步得到∠FBA=∠DBC，进而完成证明；

(2)由圆内接四边形的对角互补，可得∠CAD+∠CFD=180°，∠ADF+∠ACF=180°，进而确定∠CFD=∠PAD，∠ACF=∠PDA，再结合弧AF=弧DC，逐步确定PA=PD，即可完成证明.

（1）证明：

在同圆中，同弧所对的圆周角相等，

∠CAB=∠CFB

AB是直径，∠CAB+∠ABC=90°

又CFBD，∠DBF+∠CFB=90°

∠ABC=∠DBF

∠ABC+∠DBA=∠DBF+∠DBA

∠FBA=∠DBC

∠FBA=∠DBC

（2）证明：

圆内接四边形的对角互补，

在四边形ACFD中，∠CAD+∠CFD=180°，∠ADF+∠ACF=180°

又∠PAD+∠CAD=180°，∠PDA+∠ADF=180°

∠CFD=∠PAD，∠ACF=∠PDA.

弧AF=弧DC

∠ACF=∠DFC.

∠PDA=∠PAD

PA=PD

△PAD是等腰三角形.