题目内容
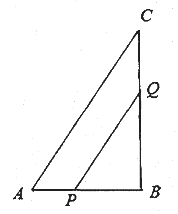
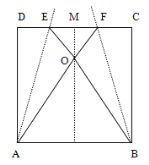
【题目】如图，先将一张边长为4的正方形纸片ABCD沿着MN对折，然后，分别将
C、D沿着折痕BF、AE对折，使得C、D两点都落在折痕MN上的点O处，则
的值为（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
先根据折叠的性质判定△ADE≌△AOE，△BFO≌△BFC；然后再根据线段的和差和勾股定理求得OM，再设DE=
，用勾股定理列出方程求出DE,OE和ME，最后比较两三角形的面积，即可完成解答.
解：
C、D沿着折痕BF、AE对折，使得C、D两点都落在折痕MN上的点O处，
△ADE≌△AOE，△BFO≌△BFC.
OA=DA=4，OE=DE
=
+
，
=
=
，
=
=
设DE=，则OE=，ME=2-
又
+
=
，
+
=
解得：=
.
又
=
=
=
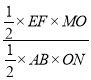
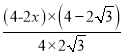将=代入，解得=
.
故选：C.
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
