ЬтФПФкШн
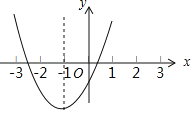
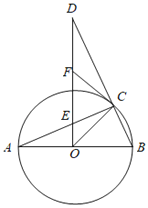
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпyЃНax2+bx+6ОЙ§ЕуAЃЈЉ3ЃЌ0ЃЉКЭЕуBЃЈ2ЃЌ0ЃЉЃЌжБЯпyЃНhЃЈhЮЊГЃЪ§ЃЌЧв0ЃМhЃМ6ЃЉгыBCНЛгкЕуDЃЌгыyжсНЛгкЕуEЃЌгыACНЛгкЕуFЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгAEЃЌЧѓhЮЊКЮжЕЪБЃЌЁїAEFЕФУцЛ§зюДѓЃЎ
ЃЈ3ЃЉвбжЊвЛЖЈЕуMЃЈЉ2ЃЌ0ЃЉЃЌЮЪЃКЪЧЗёДцдкетбљЕФжБЯпyЃНhЃЌЪЙЁїBDMЪЧЕШбќШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіhЕФжЕКЭЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
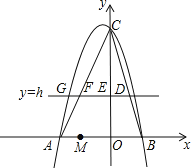
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2Љx+6ЃЛЃЈ2ЃЉЕБhЃН3ЪБЃЌЁїAEFЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ ![]() ЃЎЃЈ3ЃЉДцдкЃЌЕБhЃН
ЃЎЃЈ3ЃЉДцдкЃЌЕБhЃН![]() ЪБЃЌЕуDЕФзјБъЮЊЃЈ
ЪБЃЌЕуDЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЕБhЃН
ЃЉЃЛЕБhЃН![]() ЪБЃЌЕуDЕФзјБъЮЊЃЈ
ЪБЃЌЕуDЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉгЩЬтвтПЩЕУЕуEЕФзјБъЮЊЃЈ0ЃЌhЃЉЃЌЕуFЕФзјБъЮЊЃЈ ![]() ЃЌhЃЉЃЌИљОнSЁїAEFЃН
ЃЌhЃЉЃЌИљОнSЁїAEFЃН![]() OEFEЃН
OEFEЃН![]() h
h![]() ЃНЉ
ЃНЉ![]() ЃЈhЉ3ЃЉ2+
ЃЈhЉ3ЃЉ2+![]() ЃЎРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтОіЮЪЬтЃЎ
ЃЎРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтОіЮЪЬтЃЎ
ЃЈ3ЃЉДцдкЃЎЗжСНжжЧщаЮЧщаЮЃЌЗжБ№СаГіЗНГЬМДПЩНтОіЮЪЬтЃЎ
НтЃКШчЭМЃК
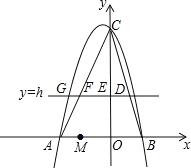
ЃЈ1ЃЉЁпХзЮяЯпyЃНax2+bx+6ОЙ§ЕуAЃЈЉ3ЃЌ0ЃЉКЭЕуBЃЈ2ЃЌ0ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЎ
ЃЎ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНЉx2Љx+6ЃЎ
ЃЈ2ЃЉЁпАбxЃН0ДњШыyЃНЉx2Љx+6ЃЌЕУyЃН6ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ6ЃЉЃЌ
ЩшОЙ§ЕуAКЭЕуCЕФжБЯпЕФНтЮіЪНЮЊyЃНmx+nЃЌдђ![]() ЃЌ
ЃЌ
НтЕУ ![]() ЃЌ
ЃЌ
ЁрОЙ§ЕуAКЭЕуCЕФжБЯпЕФНтЮіЪНЮЊЃКyЃН2x+6ЃЌ
ЁпЕуEдкжБЯпyЃНhЩЯЃЌ
ЁрЕуEЕФзјБъЮЊЃЈ0ЃЌhЃЉЃЌ
ЁрOEЃНhЃЌ
ЁпЕуFдкжБЯпyЃНh/span>ЩЯЃЌ
ЁрЕуFЕФзнзјБъЮЊhЃЌ
АбyЃНhДњШыyЃН2x+6ЃЌЕУhЃН2x+6ЃЌ
НтЕУxЃН![]() ЃЌ
ЃЌ
ЁрЕуFЕФзјБъЮЊЃЈ ![]() ЃЌhЃЉЃЌ
ЃЌhЃЉЃЌ
ЁрEFЃН![]() ЃЎ
ЃЎ
ЁрSЁїAEFЃН![]() OEFEЃН
OEFEЃН![]() h
h![]() ЃНЉ
ЃНЉ![]() ЃЈhЉ3ЃЉ2+
ЃЈhЉ3ЃЉ2+![]() ЃЌ
ЃЌ
ЁпЉ![]() ЃМ0Чв0ЃМhЃМ6ЃЌ
ЃМ0Чв0ЃМhЃМ6ЃЌ
ЁрЕБhЃН3ЪБЃЌЁїAEFЕФУцЛ§зюДѓЃЌзюДѓУцЛ§ЪЧ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉДцдкЗћКЯЬтвтЕФжБЯпyЃНhЃЎ
ЁпBЃЈ2ЃЌ0ЃЉЃЌCЃЈ0ЃЌ6ЃЉЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊyЃНЉ3x+6ЃЌЩшDЃЈmЃЌЉ3m+6ЃЉЃЎ
ЂйЕБBMЃНBDЪБЃЌЃЈmЉ2ЃЉ2+ЃЈЉ3m+6ЃЉ2ЃН42ЃЌ
НтЕУmЃН![]() Лђ
Лђ![]() ЃЈЩсЦњЃЉЃЌ
ЃЈЩсЦњЃЉЃЌ
ЁрDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌДЫЪБhЃН
ЃЉЃЌДЫЪБhЃН![]() ЃЎ
ЃЎ
ЂкЕБMDЃНBMЪБЃЌЃЈm+2ЃЉ2+ЃЈЉ3m+6ЃЉ2ЃН42ЃЌ
НтЕУmЃН![]() Лђ2ЃЈЩсЦњЃЉЃЌ
Лђ2ЃЈЩсЦњЃЉЃЌ
ЁрDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌДЫЪБhЃН
ЃЉЃЌДЫЪБhЃН![]() ЃЎ
ЃЎ
ЁпзлЩЯЫљЪіЃЌДцдкетбљЕФжБЯпyЃН![]() ЛђyЃН
ЛђyЃН![]() ЃЌЪЙЁїBDMЪЧЕШбќШ§НЧаЮЃЌЕБhЃН
ЃЌЪЙЁїBDMЪЧЕШбќШ§НЧаЮЃЌЕБhЃН![]() ЪБЃЌЕуDЕФзјБъЮЊЃЈ
ЪБЃЌЕуDЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЕБhЃН
ЃЉЃЛЕБhЃН![]() ЪБЃЌЕуDЕФзјБъЮЊЃЈ
ЪБЃЌЕуDЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ

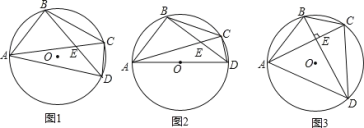
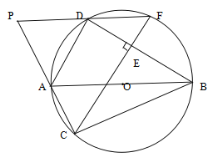
ЁОЬтФПЁПЃЈ1ЃЉШчЭМ1ЃЌЁЯA=60Ёу,AC=1ЃЌAB=2ЧѓBCЕФГЄ;
ЃЈ2ЃЉШчЭМ2ЃЌдкЁїABCжаЃЌЪджЄУї:BC2=AC2+AB2-2AC![]() ABcosA.
ABcosA.
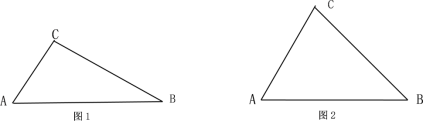
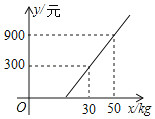
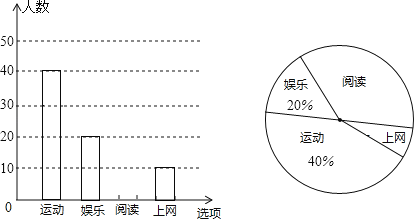
ЁОЬтФПЁПФГТУПЭаЏДјxkgЕФааРюГЫЗЩЛњЃЌЕЧЛњЧАЃЌТУПЭПЩбЁдёЭадЫЛђПьЕнааРюЃЌЭадЫЗбy1(дЊ)гыааРюжиСПxkgЕФЖдгІЙиЯЕгЩШчЭМЫљЪОЕФвЛДЮКЏЪ§ЭМЯѓШЗЖЈЃЌЯТБэСаГіСЫПьЕнЗбy2(дЊ)гыааРюжиСПxkgЕФЖдгІЙиЯЕЃЎ
ааРюЕФжиСПxkg | ПьЕнЗб |
ВЛГЌЙ§1kg | 10дЊ |
ГЌЙ§1kgЕЋВЛГЌЙ§5kgЕФВПЗж | 3дЊ/kg |
ГЌЙ§5kgЕЋВЛГЌЙ§15kgЕФВПЗж | 5дЊ/kg |
(1)ШчЙћТУПЭбЁдёЕЅЭадЫЃЌЧѓПЩаЏДјЕФУтЗбааРюЕФзюДѓжиСПЮЊЖрЩйkgЃП
(2)ШчЙћТУПЭбЁдёПьЕнЃЌЕБ1ЃМxЁм15ЪБЃЌжБНгаДГіПьЕнЗбy2(дЊ)гыааРюЕФжиСПxkgжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(3)ФГТУПЭаЏДј25kgЕФааРюЃЌЩшЭадЫmkgааРю(10ЁмmЃМ24ЃЌmЮЊе§ећЪ§)ЃЌЪЃЯТЕФааРюбЁдёПьЕнЃЌЕБmЮЊКЮжЕЪБЃЌзмЗбгУyЕФжЕзюаЁЃПВЂЧѓГіЦфзюаЁжЕЪЧЖрЩйдЊЃП