题目内容
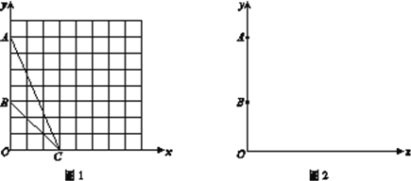
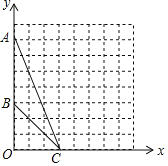
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点
),点![]() 的坐标为(
的坐标为(![]() ,
,![]() ),点C的坐标为(
),点C的坐标为(![]() ,
,![]() ).
).
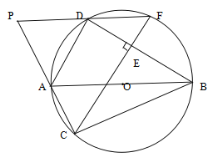
(1)在图中作出![]() 的外接圆(利用格图确定圆心);
的外接圆(利用格图确定圆心);
(2)圆心坐标为 _____;外接圆半径![]() 为 _____;
为 _____;
(3)若在![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() ,且
,且![]() ,则点
,则点![]() 的坐标为 _____.
的坐标为 _____.
【答案】(1)确定圆心,画出圆见解析;(2)圆心坐标(5,5),半径为![]() ;(3)点D的坐标(7,0).
;(3)点D的坐标(7,0).
【解析】
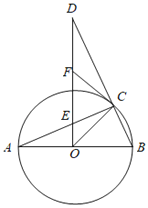
(1)分别作三角形任意两边的垂直平分线,其交点即为圆心,到三角形三顶点的距离为半径作圆即可;(2)通过A,B,C三点坐标分别算出AB和BC的垂直平分线解析式,交点即为圆心,根据勾股定理算出圆心到C点的距离即为半径;(3)要使在![]() 轴的正半轴上有一点
轴的正半轴上有一点![]() ,且
,且![]() ,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),根据ED=r解出即可.
,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),根据ED=r解出即可.
(1)分别作三角形任意两边的垂直平分线,其交点即为圆心,到三角形三顶点的距离为半径作圆即可;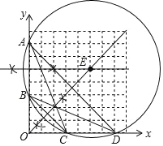
(2)∵点![]() 的坐标为(0,7),点
的坐标为(0,7),点![]() 的坐标为(0,3),点C的坐标为(3,0),
的坐标为(0,3),点C的坐标为(3,0),
∴AB的垂直平分线为y=5,
设BC的解析式为y=kx+b,把B(0,3),C(3,0)代入解得y=-x+3,则BC的垂直平分线的k=1,BC的中点坐标为(![]() ),则BC的垂直平分线为y=x,
),则BC的垂直平分线为y=x,
则y=5与y=x的交点为(5,5),故圆心为(5,5),
记圆心为点E,则EC=![]() =
=![]() ,即半径r=
,即半径r=![]() ;
;
(3)要使在x轴的正半轴上有一点D,且![]() ,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),则ED=
,根据圆周角定理知圆与x轴的另一交点即为D,设D点坐标为(x,0),则ED=![]() =
=![]() ,解得x1=3,x2=7,x=3为C点,则D点坐标为(7,0).
,解得x1=3,x2=7,x=3为C点,则D点坐标为(7,0).

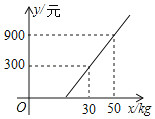
【题目】某旅客携带xkg的行李乘飞机,登机前,旅客可选择托运或快递行李,托运费y1(元)与行李重量xkg的对应关系由如图所示的一次函数图象确定,下表列出了快递费y2(元)与行李重量xkg的对应关系.
行李的重量xkg | 快递费 |
不超过1kg | 10元 |
超过1kg但不超过5kg的部分 | 3元/kg |
超过5kg但不超过15kg的部分 | 5元/kg |
(1)如果旅客选择单托运,求可携带的免费行李的最大重量为多少kg?
(2)如果旅客选择快递,当1<x≤15时,直接写出快递费y2(元)与行李的重量xkg之间的函数关系式;
(3)某旅客携带25kg的行李,设托运mkg行李(10≤m<24,m为正整数),剩下的行李选择快递,当m为何值时,总费用y的值最小?并求出其最小值是多少元?