Question

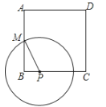
【题目】如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P.当⊙P与正方形ABCD的边相切时，BP的长为（ ）

A. 3B. 或6C. D. 3或

Answer 1

【答案】D

【解析】

分两种情形分别求 如图1中，当⊙P与直线CD相切时；如图2中当⊙P与直线AD相切时．设切点为K，连接PK，则PK⊥AD，四边形PKDC是矩形；

如图1中，当⊙P与直线CD相切时，设PC=PM=x.

在Rt△PBM中,∵PM2=BM2+PB2，

∴x2=42+(8x)2，

∴x=5，

∴PC=5，BP=BCPC=85=3.

如图2中当⊙P与直线AD相切时，设切点为K，连接PK，则PK⊥AD，四边形PKDC是矩形.

∴PM=PK=CD=2BM，

∴BM=4，PM=8，

在Rt△PBM中,PB=.

综上所述，BP的长为3或.

故选D.