Question

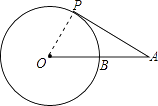
【题目】如图，已知线段OA交⊙O于点B，且OB=AB，点P是⊙O上的一个动点，那么∠OAP的最大值是（ ）
A.30°
B.45°
C.60°
D.90°

Answer 1

【答案】A
【解析】解：根据题意知，当∠OAP取最大值时，OP⊥AP；

在Rt△AOP中，∵OP=OB，OB=AB，

∴OA=2OP，

∴∠OAP=30°．

故选A．

【考点精析】本题主要考查了直线与圆的三种位置关系和切线的性质定理的相关知识点，需要掌握直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点；切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题．