题目内容
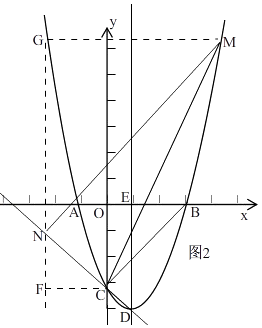
【题目】如图，抛物线y=x2+bx+c与x轴交于A（﹣1，0）和B（3，0）两点，与y轴交于点C，对称轴与x轴交于点E，点D为顶点，连接BD、CD、BC．
（1）求二次函数解析式及顶点坐标；
（2）点P为线段BD上一点，若S△BCP= 
，求点P的坐标；
（3）点M为抛物线上一点，作MN⊥CD，交直线CD于点N，若∠CMN=∠BDE，请直接写出所有符合条件的点M的坐标．
【答案】
（1）解：把A（﹣1，0）和B（3，0）两点代入抛物线y=x2+bx+c中得：
，解得： 
，
∴抛物线的解析式为：y=x2﹣2x﹣3=（x﹣1）2﹣4，
∴D（1，﹣4）
（2）解：C（0，﹣3），由勾股定理得：BC2=32+32=18，
CD2=12+（4﹣3）2=2，
BD2=（3﹣1）2+42=20，
∴CD2+BC2=BD2，
即∠BCD=90°，
∴△BCD是直角三角形；
∴S△BCD=3
由S△BCP= 
，
∴P为BD中点．
∴P（2，﹣2）
（3）解：∵∠CMN=∠BDE，
∴tan∠BDE=tan∠CMN= 
= 
，
∴ 
= ，
同理得：CD的解析式为：y=﹣x﹣3，
设N（a，﹣a﹣3），M（x，x2﹣2x﹣3），
①如图2，过N作GF∥y轴，过M作MG⊥GF于G，过C作CF⊥GF于F，
则△MGN∽△NFC，
∴ 
=2，
∴ 
= 
=2，
则 
，
∴x1=0（舍），x2=5，
当x=5时，x2﹣2x﹣3=12，
∴M（5，12），
②如图3，过N作FG∥x轴，交y轴于F，过M作MG⊥GF于G，
∴△CFN∽△NGM，
∴ 
= ，
∴ 
= 
= ，则 
∴x1=0（舍），x2= 
，
当x= 时，y=x2﹣2x﹣3=﹣ 
，
∴M（ ，﹣ ），
综上所述，点M的坐标（5，12）或（ ，﹣ ）．
【解析】（1）利用待定系数法即可得出结论，进而配成顶点式，得出顶点坐标；
（2）先利用勾股定理逆定理判断出△BCD是直角三角形，进而判断出点P是BD的中点，即可得出结论；
（3）先求出CD的解析式，再分点N在线段CD上和CD的延长线上，构造相似三角形即可得出结论。
【考点精析】本题主要考查了确定一次函数的表达式和勾股定理的逆定理的相关知识点，需要掌握确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法；如果三角形的三边长a、b、c有下面关系：a2+b2=c2，那么这个三角形是直角三角形才能正确解答此题．
