题目内容
【题目】问题背景:(1)已知A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出这几个点,并分别找到线段AB和CD中点P1、P2,然后写出它们的坐标,则P1 ,P2 .
探究发现:(2)结合上述计算结果,你能发现若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为 .
拓展应用:(3)利用上述规律解决下列问题:已知三点E(﹣1,2),F(3,1),G(1,4),第四个点H(x,y)与点E、点F、点G中的一个点构成的线段的中点与另外两个端点构成的线段的中点重合,求点H的坐标.

【答案】(1)(2,2),(﹣1,﹣2);(2)![]() ;(3)(1,﹣1)或(5,3)或(﹣3,5)
;(3)(1,﹣1)或(5,3)或(﹣3,5)
【解析】
(1)根据坐标的确定方法直接描点,分别读出各点的纵横坐标,即可得到各中点的坐标;
(2)根据(1)中的坐标与中点坐标找到规律;
(3)利用(2)中的规律进行分类讨论即可答题.
(1)如图:A(1,2),B(3,2),C(1,﹣1),D(﹣3,﹣3).在平面直角坐标系中描出它们如下:
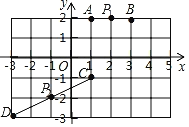
线段AB和CD中点P1、P2的坐标分别为(2,2)、(﹣1,﹣2)
故答案为:(2,2)、(﹣1,﹣2).
(2)若线段的两个端点的坐标分别为(x1,y1),(x2,y2),则线段的中点坐标为(![]() ,
,![]() ).
).
故答案为:![]() .
.
(3)∵E(﹣1,2),F(3,1),G(1,4),
∴EF、FG、EG的中点分别为:(1,![]() )、(2,
)、(2,![]() )、(0,3)
)、(0,3)
∴①HG过EF中点(1,![]() )时,
)时,![]() =1,
=1,![]() =
=![]()
解得:x=1,y=﹣1,故H(1,﹣1);
②EH过FG中点(2,![]() )时,
)时,![]() =2,
=2,![]() =
=![]()
解得:x=5,y=3,故H(5,3);
③FH过EG的中点(0,3)时,![]() =0,
=0,![]() =3
=3
解得:x=﹣3,y=5,故H(﹣3,5).
∴点H的坐标为:(1,﹣1)或(5,3)或(﹣3,5).

【题目】为了激发学生爱数学、学数学、用数学的热情,某学校在七年级开展“魅力数学”趣味竞赛,该校七年级共有学生400人参加竞赛.现随机抽取40名参赛学生的成绩数据(百分制)进行整理、描述和分析.
74 97 96 89 98 74 69 76 72 78
99 72 97 76 99 74 99 73 98 74
76 88 93 65 78 94 89 68 95 50
89 88 89 89 77 94 87 88 92 91
范围 | 50≤x≤59 | 60≤x≤69 | 70≤x≤79 | 80≤x≤89 | 90≤x≤100 |
频数 | 1 | m | 13 | 9 | 14 |
平均数、中位数、众数如下表所示:
平均数 | 中位数 | 众数 |
84.1 | n | 89 |
根据以上信息,回答下列问题:
(1)m= ,n= ;
(2)小明说:“这次竞赛我得了84分,在所有参赛学生中排名属中等偏上!”小明的说法 (填“正确”或“不正确”),理由是 ;
(3)若成绩不低于85分可以进入决赛,估计参赛的400名学生中能进入决赛的人数.
【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?



