��Ŀ����
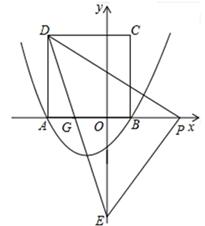
��ͼ�����κ��� ��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��1����ֱ��д����D�����꣺�� ����
��2������P���߶�AO����P����A��O�غϣ����˶����δ�ʱ���߶�OE�ij������ֵ�����������ֵ��
��3���Ƿ���������ĵ�P��ʹ��PED�ǵ��������Σ������ڣ��������P�����꼰��ʱ��PED��������ABCD�ص����ֵ�������������ڣ���˵�����ɣ�
�⣺��1������3��4����
��2����PA=t��OE=m��
�ɡ�DAP=��POE=��DPE=90��á�DAP�ס�POE��
��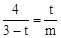 ��
��
��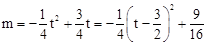 ��
��
�൱t=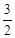 ʱ��m�����ֵ
ʱ��m�����ֵ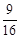 ����PΪAO�е�ʱ��OE�����ֵΪ
����PΪAO�е�ʱ��OE�����ֵΪ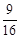 ��
��
��3�����ڡ�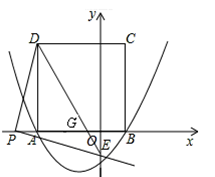
�ٵ�P��y�����ʱ��P�������Ϊ����4��0����
�ɡ�PAD�ס�OEG��OE=PA=1����OP=OA+PA=4��
�ߡ�ADG�ס�OEG����AG��GO=AD��OE=4��1��
��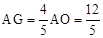 ��
��
���ص����ֵ����=S��PAG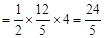 ��
��
�ڵ�P����y���Ҳ�ʱ��P�������Ϊ��4��0����
�¢ٲ��裬��ʱ�ص����ֵ����Ϊ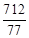 ��
��
����

ij��������ijƷ�ƵĻ��۵ƣ��������۵ư������ֳ�15���ȼ����ȼ�Խ�ߣ�����Խ�ã��磺������Ʒ����һ����Ʒ�����������������۵ƣ�һ����Ʒÿ̨�ɻ���21Ԫ��ÿ���һ���ȼ�ÿ̨�ɶ������1Ԫ������ÿ��ֻ������ͬһ���ȼ��Ļ��۵ƣ�ÿ���ȼ�ÿ��������̨�����±���ʾ��
| �ȼ���x���� | һ�� | ���� | ���� | �� |
| ��������y̨/�죩 | 78 | 76 | 74 | �� |
 ��
�� ֮��ĺ�����ϵʽ��_____��
֮��ĺ�����ϵʽ��_____����2��ÿ̨���۵ƿɻ���z��Ԫ�����ڵȼ�x�������ĺ�����ϵʽ��______��
��3���������������������Ļ��۵�ȫ���۳�������Ӧ������һ�ȼ��Ļ��۵ƣ����ܻ�����������������Ƕ��٣�

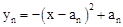 ��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1��������
��nΪ����������0<a1<a2<��<an����x��Ľ���ΪAn-1��bn-1,0����An(bn��0)����n=1ʱ����1�������� ��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ�
��x��Ľ���ΪA0��0��0����A1��b1��0���������������ƣ� ��x���ཻ�ڵ�A��B����y���ཻ�ڵ�C�������ߵĶԳ�����x���ཻ�ڵ�M��P����������x���Ϸ���һ�����㣨��P��M��C����ͬһ��ֱ���ϣ����ֱ����A��B��ֱ��CP�Ĵ��ߣ�����ֱ�ΪD��E�����ӵ�MD��ME��
��x���ཻ�ڵ�A��B����y���ཻ�ڵ�C�������ߵĶԳ�����x���ཻ�ڵ�M��P����������x���Ϸ���һ�����㣨��P��M��C����ͬһ��ֱ���ϣ����ֱ����A��B��ֱ��CP�Ĵ��ߣ�����ֱ�ΪD��E�����ӵ�MD��ME��
 �Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ
�Ķ���ΪA����y��Ľ���ΪB������AB��AC��AB����y���ڵ�C���ӳ�CA����D��ʹAD=AC������BD����AE��x�ᣬDE��y�ᣮ

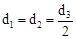 �������ڣ���ֱ��д��d3��ֵ���������ڣ���˵�����ɣ�
�������ڣ���ֱ��д��d3��ֵ���������ڣ���˵�����ɣ� ��������y�ύ�ڵ�C��0��2������x�ύ��A��B���㣨��A�ڵ�B����ߣ���
��������y�ύ�ڵ�C��0��2������x�ύ��A��B���㣨��A�ڵ�B����ߣ���

 ��
��