题目内容
如图,已知抛物线y=ax2+bx﹣4经过A(﹣8,0),B(2,0)两点,直线x=﹣4交x轴于点C,交抛物线于点D.
(1)求该抛物线的解析式;
(2)点P在抛物线上,点E在直线x=﹣4上,若以A,O,E,P为顶点的四边形是平行四边形,求点P的坐标;
(3)若B,D,C三点到同一条直线的距离分别是d1,d2,d3,问是否存在直线l,使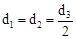 ?若存在,请直接写出d3的值;若不存在,请说明理由.
?若存在,请直接写出d3的值;若不存在,请说明理由.
解:(1)∵抛物线y=ax2+bx﹣4经过A(﹣8,0),B(2,0)两点,
∴ ,解得:
,解得: 。
。
∴抛物线的解析式为 。
。
(2)∵点P在抛物线上,点E在直线x=﹣4上,
设点P的坐标为(m, ,点E的坐标为(﹣4,n),
,点E的坐标为(﹣4,n),
如图1,∵点A(﹣8,0),∴AO=8。
①当AO为一边时,EP∥AO,且EP=AO=8,
∴|m+4|=8,解得:m1=﹣12,m2=4。
∴P1(﹣12,14),P2(4,6)。
②当AO为对角线时,则点P和点E必关于点C成中心对称,故CE=CP。
∴ ,解得:
,解得: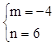 。
。
∴P3(﹣4,﹣6)。
综上所述,当P1(﹣12,14),P2(4,6),P3(﹣4,﹣6)时,A,O,E,P为顶点的四边形是平行四边形。
(3)存在4条符合条件的直线。d3的值为 。
。
解析试题分析:(1)利用待定系数法求出抛物线的解析式。
(2)平行四边形可能有多种情形,如答图1所述,需要分类讨论:
①以AO为一边的平行四边形,有2个;
②以AO为对角线的平行四边形,有1个,此时点P和点E必关于点C成中心对称。
(3)存在4条符合条件的直线。
如图2所示,连接BD,过点C作CH⊥BD于点H,
由题意得C(﹣4,0),B(2,0),D(﹣4,﹣6),
∴OC=4,OB=2,CD=6。∴△CDB为等腰直角三角形。
∴CH=CD•sin45°=6× =
= 。
。
∵BD=2CH,∴BD=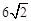 。
。
①∵CO:OB=2:1,
∴过点O且平行于BD的直线l1满足条件。
作BE⊥直线l1于点E,DF⊥直线l1于点F,设CH交直线l1于点G,
∴BE=DF,即:d1=d2。
则 ,即
,即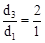 ,∴d3=2d1,∴
,∴d3=2d1,∴ 。
。
∴CG= CH,即d3=
CH,即d3= 。
。
②如图2,在△CDB外作直线l2∥DB,延长CH交l2于点G′,使CH=HG′,
∴d3=CG′=2CH=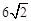 。
。
③如图3,过H,O作直线l3,作BE⊥l3于点E,DF⊥l3于点F,CG⊥l3于点G,
由①可知,DH=BH,则BE=DF,即:d1=d2.
∵CO:OB=2:1,∴ 。
。
作HI⊥x轴于点I,
∴HI=CI= CB=3,∴OI=4﹣3=1。
CB=3,∴OI=4﹣3=1。
∴ 。
。
∵△OCH的面积=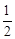 ×4×3=
×4×3= ×d3,∴d3=
×d3,∴d3= 。
。
④如图3,根据等腰直角三角形的对称性,可作出直线l4,易证: ,d3=
,d3= 。
。
综上所述,存在直线l,使 .d3的值为:
.d3的值为: 。
。

“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
| 时段 | x | 还车数(辆) | 借车数(辆) | 存量y(辆) |
| 6:00﹣7:00 | 1 | 45 | 5 | 100 |
| 7:00﹣8:00 | 2 | 43 | 11 | n |
| … | … | … | … | … |
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:00这个时段的还车数比借车数的3倍少4,求此时段的借车数.

 为顶点,且过点
为顶点,且过点 .
. )三点.
)三点.
 的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
的图象与x轴交于点A(﹣3,0)和点B,以AB为边在x轴上方作正方形ABCD,点P是x轴上一动点,连接DP,过点P作DP的垂线与y轴交于点E.
 ,同理
,同理 ,所以AB的中点坐标为
,所以AB的中点坐标为 .由勾股定理得
.由勾股定理得 ,所以A、B两点间的距离公式为
,所以A、B两点间的距离公式为 .
.

 经过B,H, D三点,求抛物线解析式;
经过B,H, D三点,求抛物线解析式;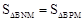 如果存在,求出点P的坐标;如果不存在,请说明理由.
如果存在,求出点P的坐标;如果不存在,请说明理由.
