��Ŀ����
��ͼ���ڡ�ABC�У���C=90�㣬BC=3��AB=5����P�ӵ�B��������ÿ��1����λ������B��C��A��B�ķ����˶�����Q�ӵ�C��������ÿ��2����λ��C��A��B������˶��������B������ԭ�ٷ��أ���P��Q����ͬʱ�˶���������ͬʱֹͣ�����˶�ʱ��Ϊt�룮
��1����t=�� ��ʱ����P���Q������
��2���ڵ�P�ӵ�B����C���˶������У�����Ϊ��ֵʱ����PCQΪ���������Σ�
��3���ڵ�Q�ӵ�B���ص�A���˶������У����PCQ�����Ϊsƽ����λ��
����s���֮��ĺ�����ϵʽ��
�ڵ�s���ʱ������P��ֱ�߽�AB�ڵ�D������ABC����ֱ��PD�۵���ʹ��A����ֱ��PC�ϣ����۵����
��APD���PCQ�ص����ֵ������
�⣺��1��7��
��2����P��B��C��ʱ����3�룬��ʱ��Q��AB�ϣ���
�� ʱ����P��BC�ϣ���Q��CA�ϣ�����PCQΪ���������Σ���һ��Ϊ����ֱ�������Σ��У�PC=CQ����3��t=2t����ã�t=1��
ʱ����P��BC�ϣ���Q��CA�ϣ�����PCQΪ���������Σ���һ��Ϊ����ֱ�������Σ��У�PC=CQ����3��t=2t����ã�t=1��
��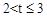 ʱ����P��BC�ϣ���Q��AB�ϣ�����PCQΪ���������Σ���һ����PQ=PC����ͼ1�������Q��PC���д����ϡ�
ʱ����P��BC�ϣ���Q��AB�ϣ�����PCQΪ���������Σ���һ����PQ=PC����ͼ1�������Q��PC���д����ϡ�
��QH��AC����QH= PC����AQH�ס�ABC��
PC����AQH�ס�ABC��
��Rt��AQH��AQ=2t��4��
�� ��
��
��PC=BC��BP=3��t��
�� ����ã�
����ã� ��
��
�����������ڵ�P�ӵ�B����C���˶������У���t=1�� ʱ����PCQΪ���������Ρ�
ʱ����PCQΪ���������Ρ�
��3���ڵ�Q�ӵ�B���ص�A���˶������У�Pһ����AC�ϣ�
��PC=t��3��BQ=2t��9���� ��
��
ͬ��2���ɵã���PCQ�У�PC���ϵĸ��ǣ� ��
��
�� ��
��
�൱t=5ʱ��s�����ֵ����ʱ��P��AC���е㣨��ͼ2����
����ֱ��PD�۵���ʹ��A����ֱ��PC�ϣ�
��PDһ����AC���д��ߡ�
��AP=CP= AC=2��PD=
AC=2��PD= BC=
BC= ��
��
��AQ=14��2t=14��2��5=4��
��ͼ2������DC����AD���۵��ߣ���PQ�ڵ�O����Q��QE��CA�ڵ�E����O��OF��CA�ڵ�F�����PCO��Ϊ�۵���ġ�APD���PCQ�ص����ֵ������
��QE= AQ=
AQ= ��4=
��4= ��EA=
��EA= AQ=
AQ= ��4=
��4= ��
��
��EP=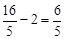 ��CE=
��CE= ��
��
��FP=x��FO=y����CF= ��
��
�ɡ�CFO�ס�CPD�� ����
���� ����
����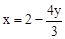 ��
��
�ɡ�PFO�ס�PEQ�� ����
���� ����
����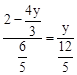 ����ã�
����ã� ��
��
���PCO��Ϊ�۵���ġ�APD���PCQ�ص����ֵ���� ��
��
���������������1���������ù��ɶ������AC�ij��ȣ���P���Q����һ������P��B��A�Ĺ����У����÷��̼�����ã�
��Rt��ABC�У��ߡ�C=90�㣬BC=3��AB=5������ݹ��ɶ�����AC=4��
��Q��C��B������·����9����Ҫ��ʱ����4.5�룬��ʱP�˶���·����4.5��P��Q֮��ľ����ǣ�3+4+5��4.5=7.5��
��������ã� ����ã�t=7��
����ã�t=7��
��2����Ϊ��P��B��C��ʱ����3�룬��ʱ��Q��AB�ϣ����Է� ����P��BC�ϣ���Q��CA�ϣ���
����P��BC�ϣ���Q��CA�ϣ���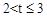 ����P��BC�ϣ���Q��AB�ϣ�������������������t��ֵ��
����P��BC�ϣ���Q��AB�ϣ�������������������t��ֵ��
��3���ڵ�Q�ӵ�B���ص�A���˶������У�Pһ����AC�ϣ���PC�ij�����t��3��Ȼ���������������ε����ʼ�������t��ʾ��s��ֵ��Ȼ�����ö��κ��������ʼ������s���ʱt��ֵ����ʱ��P��AC���е㣬ֱ��PD�۵���ʹ��A����ֱ��PC�ϣ���PDһ����AC���д��ߡ���ˣ�����DC����AD���۵��ߣ���PQ�ڵ�O����Q��QE��CA�ڵ�E����O��OF��CA�ڵ�F�����PCO��Ϊ�۵���ġ�APD���PCQ�ص����ֵ������Ӧ�á�CFO�ס�CPD�͡�PFO�ס�PEQ�ñ���ʽ���OF�ij�������á�PCO��Ϊ�۵���ġ�APD���PCQ�ص����ֵ���� ��
��

 ��������ϵ�д�
��������ϵ�д� ��x�ύ��A��B���㣬��y�ύ��C�㣬�ı���OBHCΪ���Σ�CH���ӳ��߽��������ڵ�D��5��2��������BC��AD.
��x�ύ��A��B���㣬��y�ύ��C�㣬�ı���OBHCΪ���Σ�CH���ӳ��߽��������ڵ�D��5��2��������BC��AD.
 Ϊ���㣬�ҹ���
Ϊ���㣬�ҹ��� ��
�� ��ͼ������ƽ��1����λ��������ƽ��2����λ����ƽ�ƺ�������ߵĽ���ʽ��ƽ�ƺ������ߵ���״���䣩��
��ͼ������ƽ��1����λ��������ƽ��2����λ����ƽ�ƺ�������ߵĽ���ʽ��ƽ�ƺ������ߵ���״���䣩�� ��
�� ��3����������ƽ��2����λ�õ�
��3����������ƽ��2����λ�õ� ��
�� ��0��4����������ƽ��2����λ�õ�
��0��4����������ƽ��2����λ�õ� ��0��2����
��0��2���� ��
�� ����ã�
����ã� ��
�� ��
�� ����ƽ��3����λ��������ƽ��1����λ����ƽ�ƺ��ֱ�ߵĽ���ʽ��
����ƽ��3����λ��������ƽ��1����λ����ƽ�ƺ��ֱ�ߵĽ���ʽ�� ������A��0��3����B��3��0����C��4��3����
������A��0��3����B��3��0����C��4��3����

 �����㣮
�����㣮
 ��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
��ͼ����x�ύ�ڵ�A����3��0���͵�B����ABΪ����x���Ϸ���������ABCD����P��x����һ���㣬����DP������P��DP�Ĵ�����y�ύ�ڵ�E��
