题目内容
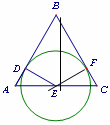
已知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒.
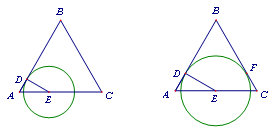
(l)如图l,判断⊙E与AB的位置关系,并证明你的结论;
(2)如图2,当⊙E与BC切于点F时,求t的值;
(3)以点C为圆心,CE长为半径作⊙C,OC与射线AC交于点G.当⊙C与⊙E相切时,直接写出t的值为____

(l)如图l,判断⊙E与AB的位置关系,并证明你的结论;
(2)如图2,当⊙E与BC切于点F时,求t的值;
(3)以点C为圆心,CE长为半径作⊙C,OC与射线AC交于点G.当⊙C与⊙E相切时,直接写出t的值为____
(1)AB与⊙E相切;(2)1;(3)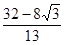 ,
,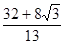
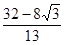 ,
,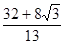
试题分析:(1)过点D作DM⊥AC于点M,先根据等边三角形的性质得到∠A=60°,在Rt△ADM中即可表示出AM、DM的长,由AE=2t可得ME=
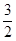 t,在Rt△DME中,DE=AM+EM=3t,在Rt△ADE中,可得AD+DE=AE,即可得到∠ADE=90°,从而证得结论;
t,在Rt△DME中,DE=AM+EM=3t,在Rt△ADE中,可得AD+DE=AE,即可得到∠ADE=90°,从而证得结论;(2)连BE、EF,根据切线的性质可得BE平分∠ABC,由AB=BC可得AE=CE,即可求得结果;
(3)当⊙C与⊙E相切时,DE=EG=2EC,分点E在线段AC上与点E在AC的延长线上两种情况分析即可.
(1)过点D作DM⊥AC于点M

∵△ABC为等边三角形
∴∠A=60°
在Rt△ADM中,AD=t,∠A=60°
∴AM=
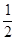 t,DM=
t,DM=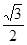 t
t∵AE=2t
∴ME=
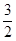 t
t在Rt△DME中,DE=AM+EM=3t
在Rt△ADE中,AD=t,AE=4t,DE=3t
∴AD+DE=AE
∴∠ADE=90°
∴AD与⊙D相切;
(2)连BE、EF,
∵BD、BE与⊙O相切
∴BE平分∠ABC
∵AB=BC
∴AE=CE
∵AC=4
∴AE=2,t=1;
(3)当⊙C与⊙E相切时,DE=EG=2EC
∵DE=
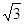 t,
t,∴EC=
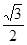 t,
t,有两种情形:
第一,当E在线段AC上时,AC=AE+EC,2t+
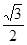 t=4,t=
t=4,t=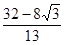
第二、当点E在AC的延长线上时,AC=AE-EC,2t-
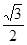 t=4,t=
t=4,t=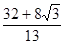 .
.点评:解答本题的关键是熟练掌握切线垂直于经过切点的半径;两圆内切时,圆心距等于两圆半径之差,两圆外切时,圆心距等于两圆半径之和.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
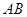 是⊙O的直径,弦BC=8,∠BOC=60°, OE⊥AC,垂足为E.
是⊙O的直径,弦BC=8,∠BOC=60°, OE⊥AC,垂足为E.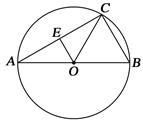

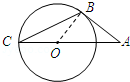
 的半径为4,
的半径为4, 是直径
是直径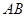 同侧圆周上的两点,弧
同侧圆周上的两点,弧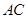 的度数为
的度数为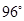 ,弧
,弧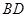 的度数为
的度数为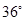 ,动点
,动点 在
在 的最小值为 。
的最小值为 。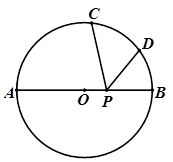



 )
)
 cm,阴影部分弓高为6,求弓形的面积;
cm,阴影部分弓高为6,求弓形的面积;