题目内容
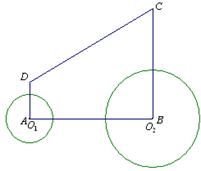
某种在同一平面进行传动的机械装置如图1,图2是它的示意图.其工作原理是:滑块Q在平直滑道l上可以左右滑动,在Q滑动的过程中,连杆PQ也随之运动,并且PQ带动连杆OP绕固定点O摆动.在摆动过程中,两连杆的接点P在以OP为半径的⊙O上运动.数学兴趣小组为进一步研究其中所蕴含的数学知识,过点O作OH ⊥l于点H,并测得OH = 4 dm,PQ = 3 dm,OP = 2 dm.解决问题


(1)点Q与点O间的最小距离是 dm;点Q与点O间的最大距离是 dm;点Q在l上滑到最左端的位置与滑到最右端位置间的距离是 分米.
(2)如图3,小明同学说:“当点Q滑动到点H的位置时,PQ与⊙O是相切的.”你认为他的判断对吗?为什么?

(3)①小丽同学发现:“当点P运动到OH上时,点P到l的距离最小.”事实上,还存在着点P到l距离最大的位置,此时,点P到l的距离是 dm;
②当OP绕点O左右摆动时,所扫过的区域为扇形,求这个扇形面积最大时圆心角的度数.


(1)点Q与点O间的最小距离是 dm;点Q与点O间的最大距离是 dm;点Q在l上滑到最左端的位置与滑到最右端位置间的距离是 分米.
(2)如图3,小明同学说:“当点Q滑动到点H的位置时,PQ与⊙O是相切的.”你认为他的判断对吗?为什么?

(3)①小丽同学发现:“当点P运动到OH上时,点P到l的距离最小.”事实上,还存在着点P到l距离最大的位置,此时,点P到l的距离是 dm;
②当OP绕点O左右摆动时,所扫过的区域为扇形,求这个扇形面积最大时圆心角的度数.
(1)4 5 6; (2)不对; (3)① 3 ②120°
试题分析:
解:(1)点Q与点O间的最小距离是OH长度,即是4dm;点Q与点O间的最大距离是OP+PQ=5dm;HQ=
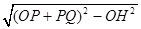 ="3dm," 点Q在l上滑到最左端的位置与滑到最右端位置间的距离是2HQ=6dm;
="3dm," 点Q在l上滑到最左端的位置与滑到最右端位置间的距离是2HQ=6dm;(2)不对.
∵OP = 2,PQ = 3,OQ = 4,且42≠32 +22,即OQ2≠PQ2 + OP2,
∴OP与PQ不垂直.∴PQ与⊙O不相切.
(3)① 3;
②由①知,在⊙O上存在点P,
 到l的距离为3,此时,OP将不能再向下转动,如图3.OP在绕点O左右摆动过程中所扫过的最大扇形就是
到l的距离为3,此时,OP将不能再向下转动,如图3.OP在绕点O左右摆动过程中所扫过的最大扇形就是 OP.连结
OP.连结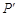 P,交OH于点D.
P,交OH于点D.∵PQ,
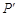
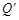 均与l垂直,且PQ =
均与l垂直,且PQ =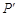
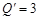 ,
,∴四边形PQ
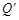
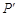 是矩形.∴OH⊥P
是矩形.∴OH⊥P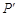 ,PD =
,PD =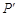 D.
D.由OP = 2,OD = OH
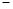 HD = 1,得∠DOP = 60°.
HD = 1,得∠DOP = 60°.∴∠PO
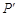 = 120°.
= 120°.∴ 所求最大圆心角的度数为120°.
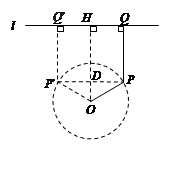
点评:垂线性质2:垂线段最短;熟记几组购股数:3、4、5;5、12、13;7、24、25.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
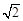 ,把△ABC绕点A 按顺时针方向旋转n 度后恰好与△ADE重合,则n的值是 ,点C经过的路线的长是 ,线段BC在上述旋转过程中所扫过部分的面积是 .
,把△ABC绕点A 按顺时针方向旋转n 度后恰好与△ADE重合,则n的值是 ,点C经过的路线的长是 ,线段BC在上述旋转过程中所扫过部分的面积是 .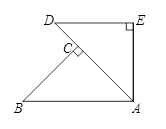
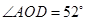 ,求
,求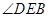 的度数;
的度数;
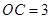 ,
,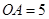 ,求
,求 的长.
的长.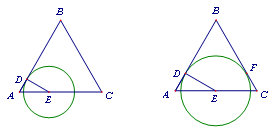
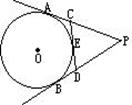
 、
、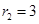 ,若两圆外切,则圆心距O1O2是( )
,若两圆外切,则圆心距O1O2是( )
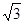 cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts.
cm/s的速度向点A运动,⊙O1半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为ts.