题目内容
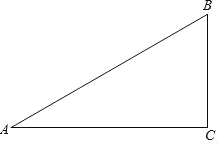
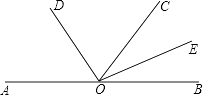
【题目】如图,在△ABC中,AC=BC,以AB为直径的⊙O交AC边于点D,点E在BC上,连结BD,DE,∠CDE=∠ABD.
(1)证明:DE是⊙O的切线;
(2)若BD=12,sin∠CDE=![]() ,求圆O的半径和AC的长.
,求圆O的半径和AC的长.
【答案】(1)详见解析;(2)圆O的半径为![]() ;AC=
;AC=![]() .
.
【解析】
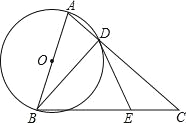
试题分析:(1)连结OD,如图,根据圆周角定理,由AB为⊙O的直径得∠ADO+∠ODB=90°,再由OB=OD得∠OBD=∠ODB,则∠ADO+∠ABD=90°,由于∠CDE=∠ABD,所以∠ADO+∠CDE=90°,然后根据平角的定义得∠ODE=90°,于是可根据切线的判定定理得到DE是⊙O的切线;(2)由于∠CDE=∠ABD,则sin∠CDE=sin∠ABD=![]() ,在Rt△ABD中,根据正弦的定义得sin∠ABD=
,在Rt△ABD中,根据正弦的定义得sin∠ABD=![]() =
=![]() ,设AD=5x,则AB=13x,由勾股定理得BD=12x,所以12x=12,解得x=1,得到AB=13,则圆O的半径为
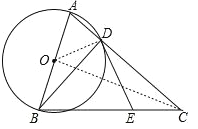
,设AD=5x,则AB=13x,由勾股定理得BD=12x,所以12x=12,解得x=1,得到AB=13,则圆O的半径为![]() ;再连结OC,如图,由于CA=CB,OA=OB,根据等腰三角形的性质得CO⊥AB,则利用等角的余角相等可得到∠ACO=∠ABD,然后在Rt△ACO中,利用∠ACO的正弦可计算出AC的长.
;再连结OC,如图,由于CA=CB,OA=OB,根据等腰三角形的性质得CO⊥AB,则利用等角的余角相等可得到∠ACO=∠ABD,然后在Rt△ACO中,利用∠ACO的正弦可计算出AC的长.
试题解析:(1)证明:连结OD,如图,
∵AB为⊙O的直径,
∴∠ADB=90°,即∠ADO+∠ODB=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ADO+∠ABD=90°,
∵∠CDE=∠ABD,
∴∠ADO+∠CDE=90°,
∴∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵∠CDE=∠ABD,
∴sin∠CDE=sin∠ABD=![]() ,
,
在Rt△ABD中,sin∠ABD=![]() =
=![]() ,
,
设AD=5x,则AB=13x,
∴BD=![]() =12x,
=12x,
∴12x=12,解得x=1,
∴AB=13,
∴圆O的半径为![]() ;
;
连结OC,如图,
∵CA=CB,OA=OB,
∴CO⊥AB,
∴∠ACO=∠ABD,
在Rt△ACO中,∵sin∠ACO=![]() =
=![]() ,
,
∴AC=![]() ×
×![]() =
=![]() .
.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
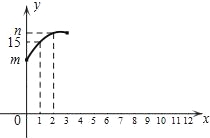
快乐暑假暑假能力自测中西书局系列答案【题目】为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
时段 | x | 还车数 | 借车数 | 存量y |
7:00﹣8:00 | 1 | 7 | 5 | 15 |
8:00﹣9:00 | 2 | 8 | 7 | n |
… | … | … | … | … |
根据所给图表信息,解决下列问题:
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00﹣11:00这个时段的还车数比借车数的2倍少4,求此时段的借车数.