题目内容
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠COB的平分线. 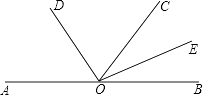
(1)求∠DOE的度数;
(2)如果∠AOD=51°17′,求∠BOE的度数.
【答案】
(1)解:∵∠AOC+∠COB=180°,已知OD是∠AOC的平分线,OE是∠COB的平分线,
∴∠DOC= ![]() ∠AOC,∠COE=
∠AOC,∠COE= ![]() ∠COB,
∠COB,
∴∠DOE=∠DOC+∠COE= ![]() (∠AOC+∠COB)=90°
(∠AOC+∠COB)=90°
(2)解:∵∠AOD+∠BOE=90°,∠AOD=51°17′,
∴∠BOE=90°﹣∠AOD=38°43′.
故答案为90°、38°43′
【解析】(1)由∠AOC+∠COB=180°,又知OD是∠AOC的平分线,OE是∠COB的平分线,故知∠DOE=∠DOC+∠COE= ![]() (∠AOC+∠COB),(2)由∠AOD+∠BOE=90°和∠AOD=51°17′,故能得到∠BOE的度数.
(∠AOC+∠COB),(2)由∠AOD+∠BOE=90°和∠AOD=51°17′,故能得到∠BOE的度数.
【考点精析】本题主要考查了角的平分线和角的运算的相关知识点,需要掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;角之间可以进行加减运算;一个角可以用其他角的和或差来表示才能正确解答此题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目