Question

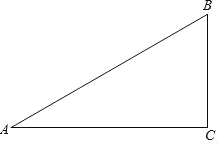
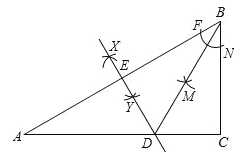
【题目】已知：如图，在△ABC中，∠A=30°，∠B=60°．

（1）作∠B的平分线BD，交AC于点D；作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作法和证明）；

（2）连接DE，求证：△ADE≌△BDE．

Answer 1

【答案】（1）详见解析；（2）详见解析.

【解析】

试题分析：（1）①以B为圆心，任意长为半径画弧，交AB、BC于F、N，再以F、N为圆心，大于FN长为半径画弧，两弧交于点M，过B、M画射线，交AC于D，线段BD就是∠B的平分线；

②分别以A、B为圆心，大于AB长为半径画弧，两弧交于X、Y，过X、Y画直线与AB交于点E，点E就是AB的中点；（2）首先根据角平分线的性质可得∠ABD的度数，进而得到∠ABD=∠A，根据等角对等边可得AD=BD，再加上条件AE=BE，ED=ED，即可利用SSS证明△ADE≌△BDE．

试题解析：（1）作出∠B的平分线BD；作出线段AB垂直平分线交AB于点E，点E是线段AB的中点．

（2）证明：

∵∠ABD=×60°=30°，∠A=30°，

∴∠ABD=∠A，

∴AD=BD，

在△ADE和△BDE中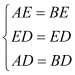

∴△ADE≌△BDE（SSS）．