题目内容
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“果圆”.如图,A,B,C,D是“果圆”与坐标轴的交点,点D的坐标为(0,8),且AB=6,点P是以AB为直径的半圆的圆心,P的坐标为(1,0),连接DB,AD,动点E,F分别从A,O两点出发,以相同的速度沿x轴正方向运动,当F到达B点时两点同时停止,过点F作FG∥BD交AD于点G.
(1)求“果圆”抛物线部分的解析式,并写出自变量的取值范围;
(2)在“果圆”上是否存在一点H,使得△DBH为直角三角形?若存在,求出H点的坐标;若不存在,说明理由;
(3)设M,N分别是GE,GF的中点,求在整个运动过程中,MN所扫过的图形面积.
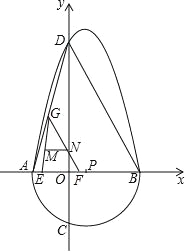
【答案】(1) 抛物线解析式为y=﹣x2+2x+8.(2) 满足条件的点H的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,5+2
,5+2![]() )或(﹣
)或(﹣![]() ,5﹣2
,5﹣2![]() ).(3)
).(3) ![]() .
.
【解析】
试题分析:(1)由题意可设抛物线解析式为y=a(x+2)(x﹣4),把点D(0,8)代入即可求出a,解决问题.(2)分三种情形讨论①D是直角顶点.②B是直角顶点.③H是直角顶点.分别求出点H坐标即可.(3)根据MN所扫过的图形是平行四边形,利用平行四边形的面积公式计算即可.
试题解析:(1)由题意,D(0,8),A(﹣2,0),B(4,0),
设抛物线解析式为y=a(x+2)(x﹣4),把点D(0,8)代入得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+8.
(2)如图1中,
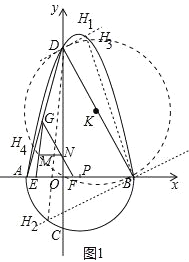
①当D为直角顶点时,
∵直线BD解析式为y=﹣2x+8,
∵DH1⊥BD,
∴直线DH1的解析式为y=![]() x+8,
x+8,
由 ,解得
,解得![]() 或
或 ,
,
∴点H1坐标为(![]() ,
,![]() ).
).
②当B为直角顶点时,直线BH2解析式为y=![]() x﹣2,设H2(m,
x﹣2,设H2(m,![]() m﹣2),
m﹣2),
由题意PH2=3,
∴(m﹣1)2+(![]() m﹣2)2=9,
m﹣2)2=9,
整理得到5m2﹣16m﹣16=0,
解得m=﹣![]() 或4,
或4,
∴点H2坐标为(﹣![]() ,﹣
,﹣![]() ).
).
③当H为直角顶点时,设H(m,﹣m2+2m+8),BD的中点K(2,4)
由题意HK=![]() BD=2
BD=2![]() ,
,
∴(m﹣2)2+(﹣m2+2m+4)2=20,
∴m(m﹣4)(m2﹣3)=0,
∴m=0或4或![]() ,
,
∴H3(![]() ,5+2
,5+2![]() ),H4的坐标为(﹣
),H4的坐标为(﹣![]() ,5﹣2
,5﹣2![]() ).
).
综上所述,满足条件的点H的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )或(
)或(![]() ,5+2
,5+2![]() )或(﹣
)或(﹣![]() ,5﹣2
,5﹣2![]() ).
).
(3)如图3中,设M1N1是起始位置,M2N2S 终止位置.
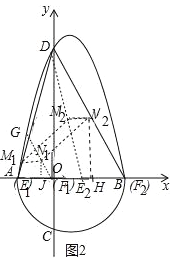
∵M1N1∥AB,M2N2∥AB,
M1N1=![]() E1F1=1,M2N2=
E1F1=1,M2N2=![]() E2F2=1,
E2F2=1,
∴M1N1∥M2N2,M1N1=M2N2,
∴四边形M1N1N2M2是平行四边形,作N1G⊥AB于J,N2H⊥AB于H.
∵DN2=BN2,HN2∥OD,
∴OH=BH,
∴HN2=![]() DO=4,
DO=4,
∵∠N1OJ=∠N2BH,∠N1JO=∠N2HB,
∴△N1JO∽△N2HB,
∴![]() ,
,
∴N1J=![]() ,
,
∴MN所扫过的图形面积就是平行四边形M1N1N2M2的面积=1×(4﹣![]() )=
)=![]() .
.

 阅读快车系列答案
阅读快车系列答案