ƒøƒ⁄»ð
°æƒø°øŒ™Ω¯“ª≤Ωª∫Ω‚≥« –ΩªÕ®—π¡¶£¨∫˛÷ðÕ∆≥ˆπ´π≤◊‘––≥µ£Æπ´π≤◊‘––≥µ‘⁄»Œ∫Œ“ª∏ˆÕ¯µÍ∂ºƒÐ µœ÷Õ®◊‚Õ®ªπ£¨ƒ≥–£—ß…˙–°√˜Õ≥º∆¡À÷С˘–£√≈ø⁄Õ£≥µÕ¯µ„∏˜ ±∂ŒµƒΩË°¢ªπ◊‘––≥µ ˝£¨“‘º∞Õ£≥µµ„’˚µ„ ±øõƒ◊‘––≥µ◊Ð ˝£®≥∆Œ™¥Ê¡ø£©«Èøˆ£¨±Ì∏Ò÷–x=1 ±µƒyµƒ÷µ±Ì æ8£∫00µ„ ±µƒ¥Ê¡ø£¨x=2 ±µƒy÷µ±Ì æ9£∫00µ„ ±µƒ¥Ê¡ø°≠“‘¥À¿ýÕ∆£¨À˚∑¢œ÷¥Ê¡øy£®¡æ£©”Îx£®xŒ™’˚ ˝£©¬˙◊„»ÁÕºÀ˘ 浃“ª∏ˆ∂˛¥Œ∫Ø ˝πÿœµ£Æ
±∂Œ | x | ªπ≥µ ˝ | ΩË≥µ ˝ | ¥Ê¡øy |
7£∫00©Å8£∫00 | 1 | 7 | 5 | 15 |
8£∫00©Å9£∫00 | 2 | 8 | 7 | n |
°≠ | °≠ | °≠ | °≠ | °≠ |
∏˘æðÀ˘∏¯Õº±Ì–≈œ¢£¨Ω‚戜¬¡–Œ £∫
£®1£©m= £¨Ω‚ Õmµƒ µº “‚“£∫ £ª
£®2£©«Û’˚µ„ ±øõƒ◊‘––≥µ¥Ê¡øy”Îx÷ƺ‰¬˙◊„µƒ∂˛¥Œ∫Ø ˝πÿœµ Ω£ª
£®3£©“—÷™10£∫00©Å11£∫00’‚∏ˆ ±∂Œµƒªπ≥µ ˝±»ΩË≥µ ˝µƒ2±∂…Ÿ4£¨«Û¥À ±∂ŒµƒΩË≥µ ˝£Æ
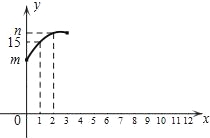
°æ¥∞∏°ø(1)13£¨7£∫00 ±◊‘––≥µµƒ¥Ê¡ø£ª(2) y=©Å![]() x2+
x2+![]() x+13£ª£®3£©10£∫00©Å11£∫00’‚∏ˆ ±∂ŒµƒΩË≥µ ˝Œ™3¡æ£Æ
x+13£ª£®3£©10£∫00©Å11£∫00’‚∏ˆ ±∂ŒµƒΩË≥µ ˝Œ™3¡æ£Æ
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©∏˘æ𵻡øπÿœµ Ω£∫m+ΩË≥µ ˝©Åªπ≥µ ˝=8£∫00µƒ¥Ê¡ø£¨¡– Ω«Û≥ˆmµƒ÷µ£¨≤¢–¥≥ˆ µº “‚“£ª£®2£©œ»«Û≥ˆ9µ„ ±◊‘––≥µµƒ¥Ê¡ø£¨µ±x=2 ±À˘∂‘”¶µƒy÷µ£¨º¥«Û≥ˆnµƒ÷µ£ª‘Ÿ…Ë“ª∞„ ΩΩ´»˝µ„◊¯±Í¥˙»Î«Û≥ˆΩ‚Œˆ Ω£ª£®3£©œ»∑÷±º∆À„9£∫00©Å10£∫00∫Õ10£∫00©Å11£∫00µƒ◊‘––≥µµƒ¥Ê¡ø£¨º¥µ±x=3∫Õx=4 ±À˘∂‘”¶µƒy÷µ£¨…Ë10£∫00©Å11£∫00’‚∏ˆ ±∂ŒµƒΩË≥µ ˝Œ™x£¨∏˘æð…œ“ª ±∂Œµƒ¥Ê¡ø+ªπ≥µ ˝©ÅΩË≥µ ˝=¥À ±∂Œµƒ¥Ê¡ø£¨¡– Ω«Û≥ˆxµƒ÷µº¥ø…£Æ
‘Ã‚Ω‚Œˆ£∫Ω‚£∫£®1£©m+7©Å5=15£¨m=13£¨
‘Úmµƒ µº “‚“£∫7£∫00 ±◊‘––≥µµƒ¥Ê¡ø£ª
π ¥∞∏Œ™£∫13£¨7£∫00 ±◊‘––≥µµƒ¥Ê¡ø£ª
£®2£©”…“‚µ√£∫n=15+8©Å7=16£¨
…Ë∂˛¥Œ∫Ø ˝µƒπÿœµ ΩŒ™£∫y=ax2+bx+c£¨
∞—£®0£¨13£©°¢£®1£¨15£©∫Õ£®2£¨16£©∑÷±¥˙»Îµ√£∫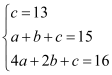 £¨
£¨
Ω‚µ√£∫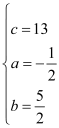 £¨
£¨
°ýy=©Å![]() x2+
x2+![]() x+13£ª
x+13£ª
£®3£©µ±x=3 ±£¨y=©Å![]() °¡32+
°¡32+![]() °¡3+13=16£¨
°¡3+13=16£¨
µ±x=4 ±£¨y=©Å![]() °¡42+
°¡42+![]() °¡4=13=15£¨
°¡4=13=15£¨
…Ë10£∫00©Å11£∫00’‚∏ˆ ±∂ŒµƒΩË≥µ ˝Œ™x£¨‘Úªπ≥µ ˝Œ™2x©Å4£¨
∏˘æð“‚µ√£∫16+2x©Å4©Åx=15£¨
x=3£¨
¥£∫10£∫00©Å11£∫00’‚∏ˆ ±∂ŒµƒΩË≥µ ˝Œ™3¡æ£Æ