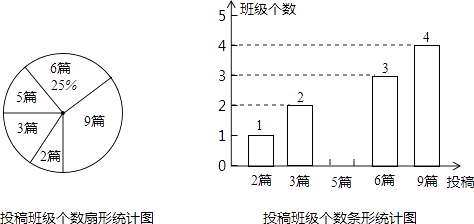
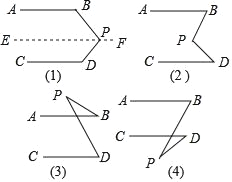
题目内容
【题目】如图,矩形ABCD中,AB=4,AD=7,点E,F分别在边AD、BC上,且B、F关于过点E的直线对称,如果以CD为直径的圆与EF相切,那么AE= . 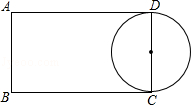
【答案】3
【解析】解:如图,设⊙O与EF相切于M,连接EB,作EH⊥BC于H. 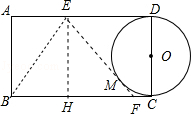
由题意易知四边形AEHB是矩形,设AE=BH=x,
由切线长定理可知,ED=EM,FC=FM,
∵B、F关于EH对称,
∴HF=BH=x,ED=EM=7﹣x,FC=FM=7﹣2x,EF=14﹣3x,
在Rt△EFH中,∵EF2=EH2+HF2 ,
∴42+x2=(14﹣3x)2 ,
解得x=3或 ![]() (舍弃),
(舍弃),
∴AE=3,
所以答案是3.
【考点精析】掌握矩形的性质和切线的性质定理是解答本题的根本,需要知道矩形的四个角都是直角,矩形的对角线相等;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目