题目内容
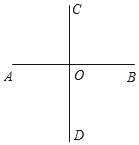
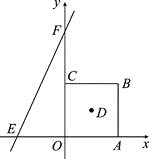
【题目】如图,在平面直角坐标系中,正方形OABC的边长为a.直线y=bx+c交x轴于E,交y轴于F,且a,b,c分别满足:-(a-4)2≥0,c=![]() +
+![]() +8.
+8.
(1)直线y=bx+c的解析式为________;正方形OABC的对角线的交点D的坐标为________;
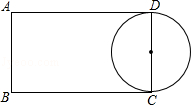
(2)若正方形OABC沿x轴负方向以每秒移动1个单位长度的速度平移,设平移的时间为t秒,问是否存在t的值,使直线EF平分正方形OABC的面积?若存在,请求出t的值;若不存在,请说明理由;
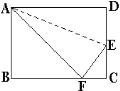
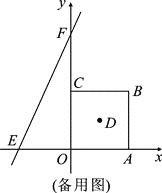
(3)点P为正方形OABC的对角线AC上的动点(端点A、C除外),PM⊥PO,交直线AB于M,在备用图中画图分析,直接写出![]() 的值.
的值.
【答案】(1)y=2x+8, D(2,2);(2)t=5;(3)![]() .
.
【解析】
(1)由已知条件易得:a=4,b=2,c=8,由此即可得到直线EF的解析式为:y=2x+8,点B的坐标为(4,4),结合点D是正方形OABC对角线的交点可得点D的坐标为(2,2);
(2)由点D是正方形OABC的对称中心可知,当点D落在直线EF上时,直线EF平分正方形OABC的面积,由已知条件设当点D落在EF上时的坐标为(2-t,2),将此坐标代入直线EF的解析式即可求得对应的t的值;
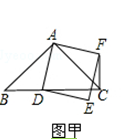
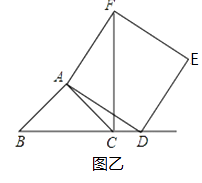
(3)如图2,过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,结合已知条件易证四边形PNCG是正方形,四边形PGBQ是矩形,四边形OHGC是矩形,PH=PQ,∠OPH=∠MPQ,由此证得△OPH≌△MPQ,从而可得QM=OH=CG=GP=BQ=![]() BM,结合PC=
BM,结合PC=![]() GP即可得到PC=
GP即可得到PC=![]() BM,由此即可得到
BM,由此即可得到![]() .
.
(1)∵![]() ,
,
∴![]() 且
且![]() ,
,
∴b=2,c=8,
∴直线y=bx+c的解析式为:y=2x+8;
∵![]() ,
,
∴![]() ,
,
∴a=4,
∴OA=AB=4,
∴点B的坐标为(4,4),
∴点D是正方形OABC对角线的交点,
∴点D是线段OB的交点,
∴点D的坐标为(2,2);
(2)存在,理由如下:
如图1,∵点D是正方形OABC的对角线的交点,
∴过点D的直线都能把正方形AOCB的面积分成相等的两部分,
∴当正方形AOCB平移到直线EF过D点时,直线正好平分正方形的面积,
设平移后的D点坐标为(2-t,2),
把它代入直线y=2x+8,2(2-t)+8=2,
解得:t=5;
(3)如图2,过P点作PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,
∵∠OPM=∠HPQ=90°,
∴∠OPH+∠HPM=90°,∠HPM+∠MPQ=90°,
∴∠OPH=∠MPQ,
∵AC为∠BAO平分线,且PH⊥OA,PQ⊥AB,
∴PH=PQ,
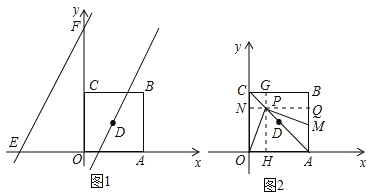
在△OPH和△MPQ中: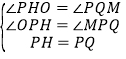
∴△OPH≌△MPQ(AAS),
∴OH=QM,
∵PQ∥OA,PH∥CO,交CO、AB于N、Q,交CB、OA于G、H,四边形AOBC是正方形,
∴易得四边形CNPG为正方形,四边形PGBQ是矩形,四边形OHGC是矩形,
∴PG=BQ=CG=OH=QM,
∴PG=![]() BM,
BM,
∵在正方形CNPG中,PC=![]() PG,
PG,
∴PC=![]() BM,
BM,
∴![]() .
.

【题目】寒假结束了,为了了解九年级学生寒假体育锻炼情况,王老师调查了九年级所有学生寒假体育锻炼时间,并随即抽取10名学生进行统计,制作出如下统计图表:
编号 | 成绩 | 编号 | 成绩 |
① | B | ⑥ | A |
② | A | ⑦ | B |
③ | B | ⑧ | C |
④ | B | ⑨ | B |
⑤ | C | ⑩ | A |
根据统计图表信息解答下列问题: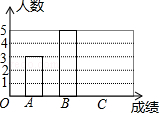
(1)将条形统计图补充完整;
(2)若用扇形统计图来描述10名学生寒假体育锻炼情况,分别求A,B,C三个等级对应的扇形圆心角的度数;
(3)已知这次统计中共有60名学生寒假体育锻炼时间是A等,请你估计这次统计中B等,C等的学生各有多少名?