题目内容
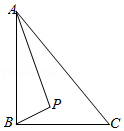
【题目】如图,已知点A是射线BE上一点,过A作CA⊥BE交射线BF于点C,AD⊥BF交射线BF于点D,给出下列结论:①∠1是∠B的余角;②图中互余的角共有3对;③∠1的补角只有∠ACF;④与∠ADB互补的角共有3个.则上述结论正确的个数有( )

A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据已知推出∠CAB=∠CAE=∠ADC=∠ADB=90°,再根据三角形内角和定理和三角形外角性质,互余、互补的定义逐个分析,即可得出答案.
∵CA⊥AB,
∴∠CAB=90°,
∴∠1+∠B=90°,即∠1是∠B的余角,∴①正确;
图中互余的角有∠1和∠B,∠1和∠DAC,∠DAC和∠BAD,共3对,∴②正确;
∵CA⊥AB,AD⊥BC,
∴∠CAB=∠ADC=90°,
∵∠B+∠1=90°,∠1+∠DAC=90°,
∴∠B=∠DAC,
∵∠CAE=∠CAB=90°,
∴∠B+∠CAB=∠DAC+∠CAE,
∴∠ACF=∠DAE,
∴∠1的补角有∠ACF和∠DAE两个,∴③错误;
∵∠CAB=∠CAE=∠ADC=∠ADB=90°,
∴与∠ADB互补的角共有3个,∴④正确;
故选C.

练习册系列答案
相关题目
【题目】甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图, 甲组12户家庭用水量统计表
用水量(吨) | 4 | 5 | 6 | 9 |
户数 | 4 | 5 | 2 | 1 |
比较5月份两组家庭用水量的中位数,下列说法正确的是( )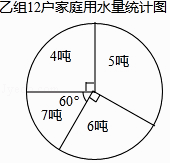
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断