题目内容
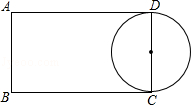
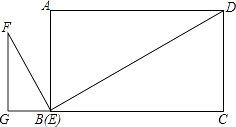
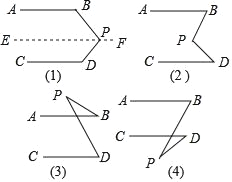
【题目】如图（1），AB∥CD，试求∠BPD与∠B、∠D的数量关系，说明理由．
（1）填空：
解：过点P作EF∥AB，
∴∠B+∠BPE=180°
∵AB∥CD，EF∥AB
∴ （如果两条直线都和第三条直线平行，那么这两条直线也互相平行）
∠EPD+ =180°
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
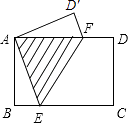
（2）依照上面的解题方法，观察图（2），已知AB∥CD，猜想图中的∠BPD与∠B、∠D的数量关系，并说明理由．
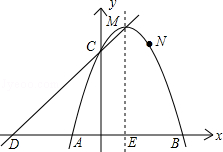
（3）观察图（3）和（4），已知AB∥CD，直接写出图中的∠BPD与∠B、∠D的数量关系，不用说明理由．
【答案】（1）CD∥EF，∠D；（2）猜想∠BPD=∠B+∠D，理由见解析；（3）∠B=∠BPD+∠D，理由见解析
【解析】
第一问利用平行线的性质解答；第二问作平行线，根据内错角相等可证∠BPD=∠B+∠D；第三问同样作平行线，根据内错角相等可证∠B=∠BPD+∠D.
（1）过点P作EF∥AB，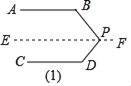
∴∠B+∠BPE=180°，
∵AB∥CD，EF∥AB，
∴CD∥EF（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD+∠D=180°，
∴∠B+∠BPE+∠EPD+∠D=360°，
∴∠B+∠BPD+∠D=360°，
故答案为：CD∥EF，∠D；
（2）猜想∠BPD=∠B+∠D，
理由：过点P作EP∥AB，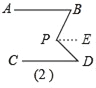
∵EP∥AB，
∴∠B=∠BPE（两直线平行，内错角相等），
∵AB∥CD，EP∥AB，
∴CD∥EP（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD=∠D，
∴∠BPD=∠B+∠D；
（3）图③结论：∠D=∠BPD+∠B，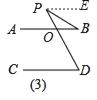
理由是：过点P作EP∥AB，
∵EP∥AB，
∴∠B=∠BPE（两直线平行，内错角相等），
∵AB∥CD，EP∥AB，
∴CD∥EP（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD=∠D，
∴∠BPD=∠B+∠D；
图④结论∠B=∠BPD+∠D，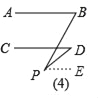
理由是：∵EP∥AB，
∴∠B=∠BPE（两直线平行，内错角相等），
∵AB∥CD，EP∥AB，
∴CD∥EP（如果两条直线都和第三条直线平行，那么这两条直线也互相平行），
∴∠EPD=∠D，
∴∠B=∠BPD+∠D．
【题目】寒假结束了，为了了解九年级学生寒假体育锻炼情况，王老师调查了九年级所有学生寒假体育锻炼时间，并随即抽取10名学生进行统计，制作出如下统计图表：
编号 | 成绩 | 编号 | 成绩 |
① | B | ⑥ | A |
② | A | ⑦ | B |
③ | B | ⑧ | C |
④ | B | ⑨ | B |
⑤ | C | ⑩ | A |
根据统计图表信息解答下列问题：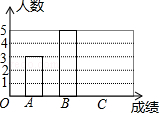
（1）将条形统计图补充完整；
（2）若用扇形统计图来描述10名学生寒假体育锻炼情况，分别求A，B，C三个等级对应的扇形圆心角的度数；
（3）已知这次统计中共有60名学生寒假体育锻炼时间是A等，请你估计这次统计中B等，C等的学生各有多少名？
