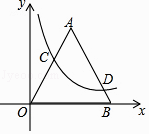题目内容
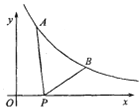
【题目】如图,已知点A(![]() ,y1)、B(2,y2)在反比例函数y=
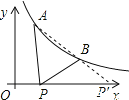
,y1)、B(2,y2)在反比例函数y=![]() 的图像上,动点P(x,0)在x轴正半轴上运动,若AP-BP最大时,则点P的坐标是 ( )
的图像上,动点P(x,0)在x轴正半轴上运动,若AP-BP最大时,则点P的坐标是 ( )
A. (![]() ,0) B. (
,0) B. (![]() ,0) C. (
,0) C. (![]() ,0) D. (1,0)
,0) D. (1,0)
【答案】B
【解析】分析:求出AB的坐标,设直线AB的解析式是y=kx+b,把A、B的坐标代入求出直线AB的解析式,根据三角形的三边关系定理得出在△ABP中,|AP﹣BP|<AB,延长AB交x轴于P′,当P在P′点时,PA﹣PB=AB,此时线段AP与线段BP之差达到最大,求出直线AB于x轴的交点坐标即可.
详解:∵把A(![]() ,y1),B(2,y2)代入反比例函数y=
,y1),B(2,y2)代入反比例函数y=![]() 得:y1=2,y2=
得:y1=2,y2=![]() ,
,
∴A(![]() ,2),B(2,
,2),B(2,![]() ),
),
∵在△ABP中,由三角形的三边关系定理得:|AP﹣BP|<AB,
∴延长AB交x轴于P′,当P在P′点时,PA﹣PB=AB,
即此时线段AP与线段BP之差达到最大,
设直线AB的解析式是y=kx+b,
把A、B的坐标代入得: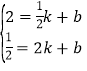 ,
,
解得:k=﹣1,b=![]() ,
,
∴直线AB的解析式是y=﹣x+![]() ,
,
当y=0时,x=![]() ,
,
即P(![]() ,0),
,0),
故选:B.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
【题目】甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图, 甲组12户家庭用水量统计表
用水量(吨) | 4 | 5 | 6 | 9 |
户数 | 4 | 5 | 2 | 1 |
比较5月份两组家庭用水量的中位数,下列说法正确的是( )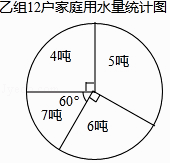
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断