题目内容
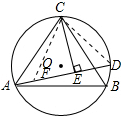
如图，等腰△ABC中，AC=BC，⊙O为△ABC的外接圆，D为
上一点，CE⊥AD于E，求证：AE=BD+DE．
 |
| BC |
证明：如图，在AE上截取AF=BD，连接CF，CD；
在△ACF和△BCD中
∴△ACF≌△BCD，
∴CF=CD，
∵CE⊥AD于E，
∴EF=DE，
∴AE=AF+EF=BD+DE．
在△ACF和△BCD中
|
∴△ACF≌△BCD，
∴CF=CD，
∵CE⊥AD于E，
∴EF=DE，
∴AE=AF+EF=BD+DE．
练习册系列答案
相关题目
线于点E．