Question

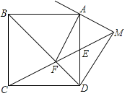
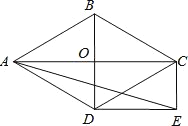
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C. D作CE∥BD,DE∥AC，CE和DE交于点E.

（1）求证：四边形ODEC是矩形；

（2）当∠ADB=60°,AD=2时，求EA的长。

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）先证四边形ODEC是平行四边形，然后根据菱形的对角线互相垂直，得到∠DOC=90°，根据矩形的定义即可判定四边形ODEC是矩形．

（2）根据含30度角直角三角形的性质、勾股定理来求EA的长度即可．

（1）∵CE∥BD,DE∥AC，

∴四边形ODEC是平行四边形，

又∵菱形ABCD，

∴AC⊥BD，∴∠DOC=90°，

∴四边形ODEC是矩形；

（2）∵Rt△AOD中,∠ADO=60°，

∴∠OAD=30°，

∴OD=AD=，

∴AO==3，

∴AC=6，

∵四边形ODEC是矩形，

∴EC=OD=，∠ACE=90°，

∴AE==.