题目内容
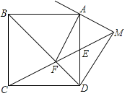
【题目】如图,边长为![]() 的正方形
的正方形![]() 中,
中,![]() 为
为![]() 的中点,连接
的中点,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 交
交![]() 的延长线于
的延长线于![]() ,则
,则![]() 的长为________.
的长为________.
【答案】![]()
【解析】
作MN⊥AD,先证明MA=ME,进而求出AN=NE=1,利用MN∥CD得:![]() ,
,
求出MN,在RT△MND中利用勾股定理即可求出DM.
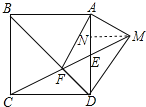
作MN⊥AD垂足为N.
∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠ABF=∠CBF,BC∥AD,∠BAD=∠CDA=90°,
∵BF=BF,
∴△BFA≌△BFC,
∴∠BAF=∠BCF=∠CED=∠AEM,
∵∠MAF=∠BAD=90°,
∴∠BAF=∠MAE,
∴∠MAE=∠AEM,
∴MA=ME
∵AE=ED=![]() AD=2,
AD=2,
∴AN=NE=![]() AE=1,
AE=1,
∵∠MNE=∠CDE=90°,
∴MN∥CD,
∴△MNE∽△CDE,
∴![]() =
=![]() ,
,
∵CD=4,
∴MN=2,
在RT△MND中,∵MN=2,DN=3,
∴DM=![]() =
=![]() =
=![]() ,
,
故答案为:![]()

练习册系列答案
相关题目