题目内容
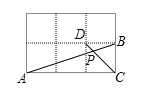
【题目】已知,如图,![]() 中,
中,![]() ,
,![]() ,
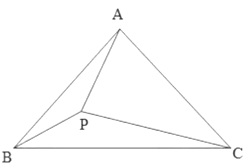
,![]() 为形内一点,若
为形内一点,若![]() ,
,![]() ,则
,则![]() 的度数为__________.
的度数为__________.
【答案】![]()
【解析】
在BC下方取一点D,使得三角形ACD为等边三角形,连接DP、BD.根据等腰三角形的性质和三角形的内角和定理证明△BDC≌△BPC和![]() ,从而可证明△BPD为等边三角形,根据等边三角形的性质可得∠BPD=60°,BP=DP,证明△ABP≌△ADP,从而可得
,从而可证明△BPD为等边三角形,根据等边三角形的性质可得∠BPD=60°,BP=DP,证明△ABP≌△ADP,从而可得![]() .
.
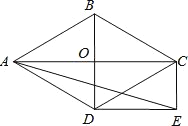
解:如下图在BC下方取一点D,使得三角形ACD为等边三角形,连接DP、BD.
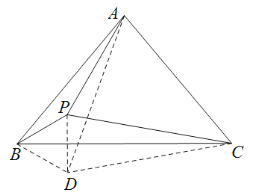
∴AD=AB=AC,∠ADC=∠CAD=60°,
∵∠BAC=80°,AB=AC,
∴∠DAB=∠BAC-∠CAD=20°,∠ABC=∠ACB=50°,
∴∠ABD=∠ADB=80°,
∴∠BDC=∠ADB+∠ADC=140°,∠DBC=∠ABD-∠ABC=30°,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵BC=BC
∴△BDC≌△BPC,
∴BD=BP,
∵![]() ,
,
∴△BPD为等边三角形,
∴∠BPD=60°,BP=DP,
在△ABP和△ADP中,
∵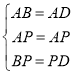
∴△ABP≌△ADP,
∴![]() .
.
故答案为:150°.

练习册系列答案
相关题目