ЬтФПФкШн
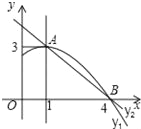
ЁОЬтФПЁПШчЭМЪЧХзЮяЯпy1=ax2+bx+cЃЈaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌгыxжсЕФвЛИіНЛЕуBЃЈ4ЃЌ0ЃЉЃЌжБЯпy2=mx+nЃЈmЁй0ЃЉгыХзЮяЯпНЛгкAЃЌBСНЕуЃЌЯТСаНсТлЃК
Ђй2a+b=0ЃЛ
ЂкabcЃО0ЃЛ
Ђлb2Љ4acЃО0ЃЛ
ЂмХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЪЧЃЈЉ1ЃЌ0ЃЉЃЛ
ЂнЕБ1ЃМxЃМ4ЪБЃЌгаy2ЃМy1ЃЛ
ЂоЗНГЬax2+bx+c=3гаСНИіЯрЕШЕФЪЕЪ§ИљЃЎ
Цфжае§ШЗЕФга_____ЃЎ
ЁОД№АИЁПЂйЂлЂнЂоЃЎ
ЁОНтЮіЁПЗжЮі: ЂйРћгУЖдГЦжсxЃН1ХаЖЈЃЛ
ЂкИљОнЭМЯѓШЗЖЈaЁЂbЁЂcЕФЗћКХЃЛ
ЂлИљОнХзЮяЯпгыxжсНЛЕуЕФИіЪ§ШЗЖЈЃЛ
ЂмИљОнЖдГЦадХаЖЯЃЛ
ЂнгЩЭМЯѓЕУГіЃЌдк1ЃМxЃМ4ЪБЃЌХзЮяЯпзмдкжБЯпЕФЩЯУцЃЌдђyЃМyЃЛ
ЂоЗНГЬax2ЃЋbxЃЋcЃН3ЕФИљЃЌОЭЪЧЭМЯѓЩЯЕБyЃН3ЪЧЫљЖдгІЕФxЕФжЕЃЎ
злЩЯМДПЩЕУГіНсТлЃЎ
ЯъНт: ЂйвђЮЊХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌЫљвдЖдГЦжсЮЊЃКxЃН1ЃЌдђ![]() ЃН1ЃЌ2aЃЋbЃН0ЃЌЙЪЂйе§ШЗЃЛ
ЃН1ЃЌ2aЃЋbЃН0ЃЌЙЪЂйе§ШЗЃЛ
ЂкЁпХзЮяЯпПЊПкЯђЯТЃЌ
ЁрaЃМ0ЃЌ
ЁпЖдГЦжсдкyжсгвВрЃЌ
ЁрbЃО0ЃЌ
ЁпХзЮяЯпгыyжсНЛгке§АыжсЃЌ
ЁрcЃО0ЃЌ
ЁрabcЃМ0ЃЌ
ЙЪЂкВЛе§ШЗЃЛ
ЂлЁпХзЮяЯпгыxжсгаСНИіНЛЕуЃЌ
Ёрb24acЃО0ЃЌ
ЙЪЂле§ШЗЃЛ
ЂмвђЮЊХзЮяЯпЖдГЦжсЪЧЃКxЃН1ЃЌBЃЈ4ЃЌ0ЃЉЃЌ
ЫљвдХзЮяЯпгыxжсЕФСэвЛИіНЛЕуЪЧЃЈ2ЃЌ0ЃЉЃЌ
ЙЪЂмВЛе§ШЗЃЛ
ЂнгЩЭМЯѓЕУЃКЕБ1ЃМxЃМ4ЪБЃЌгаy2ЃМy1ЃЛЙЪЂне§ШЗЃЛ
ЂоЁпХзЮяЯпЕФЖЅЕузјБъAЃЈ1ЃЌ3ЃЉЃЌ
ЁрЗНГЬax2ЃЋbxЃЋcЃН3гаСНИіЯрЕШЕФЪЕЪ§ИљЪЧxЃН1ЃЌ
ЙЪЂое§ШЗЃЛ
дђЦфжае§ШЗЕФгаЃКЂйЂлЂнЂоЃЛ
ЙЪД№АИЮЊЃКЂйЂлЂнЂоЃЎ
ЕуОІ: БОЬтбЁЯюНЯЖрЃЌБШНЯШнвзГіДэЃЌвђДЫвЊШЯецРэНтЬтвтЃЌУїШЗвдЯТМИЕуЪЧЙиМќЃКЂйЭЈГЃ2aЃЋbЕФжЕЖМЪЧРћгУХзЮяЯпЕФЖдГЦжсРДШЗЖЈЃЛЂкХзЮяЯпгыxжсЕФНЛЕуИіЪ§ШЗЖЈЦфЁїЕФжЕЃЌМДb4acЕФжЕЃКЁїЃНb4acЃО0ЪБЃЌХзЮяЯпгыxжсга2ИіНЛЕуЃЛЁїЃНb4acЃН0ЪБЃЌХзЮяЯпгыxжсга1ИіНЛЕуЃЛЁїЃНb4acЃМ0ЪБЃЌХзЮяЯпгыxжсУЛгаНЛЕуЃЛЂлжЊЕРЖдГЦжсКЭХзЮяЯпЕФвЛИіНЛЕуЃЌРћгУЖдГЦадПЩвдЧѓгыxжсЕФСэвЛНЛЕуЃЎ