题目内容
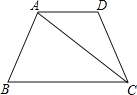
【题目】已知：在矩形ABCD中，点F为AD中点,点E为AB边上一点，连接CE、EF、CF，EF平分∠AEC.
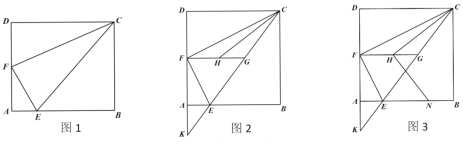
(1)如图1，求证：CF⊥EF;
(2)如图2，延长CE、DA交于点K, 过点F作FG∥AB交CE于点G若，点H为FG上一点，连接CH,若∠CHG=∠BCE, 求证：CH=FK;
(3)如图3, 过点H作HN⊥CH交AB于点N,若EN=11,FH-GH=1,求GK长.
【答案】(1)证明见解析；(2)证明见解析；(3)CN=25.
【解析】
(1)如图，延长EF交CD延长线于点Q，先证明CQ=CE，再证明△FQD≌△FEA，根据全等三角形的对应边相等可得EF=FQ，再根据等腰三角形的性质即可得CF⊥EF；
(2)分别过点F、H作FM⊥CE ，HP⊥CD，垂足分别为M、P，证明四边形DFHP是矩形，继而证明△HPC≌△FMK，根据全等三角形的性质即可得CH=FK；
(3)连接CN，延长HG交CN于点T，设∠DCF=α，则∠GCF=α， 先证明得到FG=CG=GE，∠CGT=2
，再由FG是BC的中垂线，可得BG = CG， ∠CGT=∠FGK=∠BGT=2，再证明HN∥BG，得到四边形HGBN是平行四边形，继而证明△HNC≌△KGF，推导可得出HT=CT=TN ，由FH-HG=1，所以设GH=m，则BN=m，FH=m+1，CE=2FG=4m+2，继而根据
，可得关于m的方程，解方程求得m的值即可求得答案.
(1)如图，延长EF交CD延长线于点Q，
∵矩形ABCD，AB∥CD，
∴∠AEF=∠CQE， ∠A=∠QDF，
又∵EF 平分∠AEC ，
∴∠AEF=∠CEF，
∴∠CEF=∠CQE，
∴CQ=CE，
∵点F是AD中点，
∴AF=DF，
∴△FQD≌△FEA，
∴EF=FQ，
又∵CE=CQ，
∴CF⊥EF；
(2)分别过点F、H作FM⊥CE ，HP⊥CD，垂足分别为M、P，
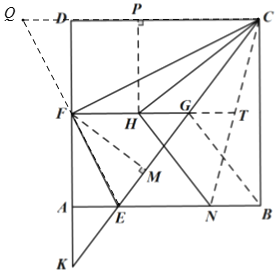
∵CQ=CE ，CF⊥EF，
∴∠DCF=∠FCE，
又∵FD⊥CD，
∴FM=DF，
∵FG//AB，∴∠DFH=∠DAC=90°，
∴∠DFH=∠FDP=∠DPH=90°，
∴四边形DFHP是矩形，
∴DF=HP，
∴FM= DF=HP，
∵∠CHG=∠BCE，AD∥BC，FG∥CD，
∴∠K=∠BCE=∠CHG=∠DCH，
又∵∠FMK=∠HPC=90°，
∴△HPC≌△FMK，
∴CH=FK；
(3)连接CN，延长HG交CN于点T，设∠DCF=α，则∠GCF=α，
∵FG∥CD ，∴∠DCF=∠CFG，
∴∠FCG=∠CFG，∴FG=CG，
∵CF⊥EF，
∴∠FEG+∠FCG=90°，∠CFG+∠GFE=90°，
∴∠GFE=∠FEG，∴GF=FE，
∴FG=CG=GE，∠CGT=2，
∵FG是BC的中垂线，
∴BG = CG， ∠CGT=∠FGK=∠BGT=2，
∵∠CHG=∠BCE=90°-2，∠CHN=90°，
∴∠GHN=∠FGK=∠BGT=2，
∴HN∥BG，
∴四边形HGBN是平行四边形，
∴HG=BN，HN=BG = CG =FG，
∴△HNC≌△KGF，
∴GK=CN，∠HNC=∠FGK=∠NHT=2，
∴HT=CT=TN ，
∵FH-HG=1，∴设GH=m，则BN=m，FH=m+1，CE=2FG=4m+2，
∵GT=
，∴CN=2HT=11+2m，
∵，
∴
∴
(舍去)，
，
∴CN=GK=2HT=25.
