题目内容
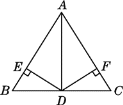
【题目】如图，AB＝AC，AD是△ABC的角平分线，DE⊥AB于E，DF⊥AC于F，则下列四个结论中：①DE＝DF；②AD上任意一点到AB，AC的距离相等；③∠BDE＝∠CDF；④BD＝CD且AD⊥BC，其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
【答案】D
【解析】
由题意知，△ABC是等腰三角形，由三线合一的性质知，点D是BC的中点，AD⊥BC，可得④正确；根据角平分线的性质可得①②正确；再由∠DEB=∠DFC=90°，∠B=∠C，根据三角形内角和定理可得③正确；故可得到4个结论均正确．
解：∵AB=AC，
∴△ABC是等腰三角形，∠B=∠C．
∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，
∴AD⊥BC，BD=CD，DE=DF，AD上任意一点到AB、AC的距离相等，故①②④正确；
∵DE⊥AB于E，DF⊥AC，
∴∠DEB=∠DFC=90°．
∵∠DEB=∠DFC=90°，∠B=∠C，
∴∠BDE=∠CDF，即③正确；
故选：D．
练习册系列答案
科学实验活动册系列答案
相关题目
