题目内容
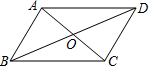
如图,以AB为直径的半圆O上有一点C,过A点作半圆的切线交BC的延长线于点D.
(1)求证:△ADC∽△BDA;
(2)过O点作AC的平行线OF分别交BC,
于E、F两点,若BC=2
,EF=1,求
的长.

(1)求证:△ADC∽△BDA;
(2)过O点作AC的平行线OF分别交BC,
 |
| BC |
| 3 |
 |
| AC |

(1)证明:∵AB为直径,
∴∠ACB=90°,
∴∠ACD=90°.
∵AD为半圆O的切线,
∴∠BAD=90°,
∴∠ACD=∠BAD.
又∵∠ADC=∠BDA,
∴△ADC∽△BDA.
(2)连接OC,
∵OE∥AC,
∴OE⊥BC,
∴BE=EC=
.
在Rt△OBE中,设OB=x,则有:x2=(
)2+(x-1)2
∴x=OB=2,
∴OE=1,
∴∠OBE=30°,
∴∠AOC=60°,
∴
的长=
=
.
∴∠ACB=90°,
∴∠ACD=90°.
∵AD为半圆O的切线,
∴∠BAD=90°,
∴∠ACD=∠BAD.
又∵∠ADC=∠BDA,
∴△ADC∽△BDA.
(2)连接OC,

∵OE∥AC,
∴OE⊥BC,
∴BE=EC=
| 3 |
在Rt△OBE中,设OB=x,则有:x2=(
| 3 |
∴x=OB=2,
∴OE=1,
∴∠OBE=30°,
∴∠AOC=60°,
∴
 |
| AC |
| 60π×2 |
| 180 |
| 2π |
| 3 |

练习册系列答案
相关题目