��Ŀ����
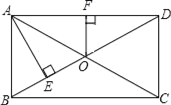
����Ŀ����֪����ͼ1����ƽ��ֱ������ϵ�У�һ�κ���![]() ��ͼ��x���ڵ�A����y���ڵ�B����C�ǵ�A����y��ԳƵĵ㣬����C��y��ƽ�е�����CD����ֱ��AB���D����P������CD�ϵ�һ�����㣮
��ͼ��x���ڵ�A����y���ڵ�B����C�ǵ�A����y��ԳƵĵ㣬����C��y��ƽ�е�����CD����ֱ��AB���D����P������CD�ϵ�һ�����㣮


��1�����A��B�����꣮
��2����ͼ2������ACP����AP���ۣ�����C�Ķ�Ӧ��E����ֱ��AB��ʱ�����P�����꣮
��3����ֱ��OP��ֱ��AD�н��㣬�����轻��ΪQ�������D�غϣ�������CQ���Ƿ���ڵ�P��ʹ��S��CPQ =2S��DPQ�������ڣ���ֱ��д����P���ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��A������Ϊ����3��0����B����Ϊ��0��4������2����P������(3��3)����3����P����Ϊ��3��![]() ����3��16��
����3��16��
��������
(1)��y=0����![]() ����ã�x=-3����x=0����
����ã�x=-3����x=0����![]() �����ɵõ��𰸣�
�����ɵõ��𰸣�
(2)�����AC=6��CD=8��AD=10������CP=y ����DP=8-y��EP=y����RtDEP�У����ݹ��ɶ������з��̣�������⣻
(3)��S��CPQ =2S��DPQʱ��CP=2DP��������������ۣ�������P���߶�CD��ʱ��������P���߶�CD���ӳ�����ʱ���������.
��1����y=0����![]() ����ã�x=-3��
����ã�x=-3��
��x=0����![]()
��A��������-3��0����B������0��4����
��2���ߵ�C�ǵ�A����y��ԳƵĵ㣬
���C�������ǣ���3��0����
��D��������3��8����
��AC=6��CD=8��AD=10��
��CP=y ����DP=8-y��EP=y��
��AE=AC=6��
��ED=AD-AE=10-6=4��
����RtDEP��![]() ��
��
��![]() ��
��
��ã�y=3��
���P������(3��3)��
��3����S��CPQ =2S��DPQʱ��CP=2DP��������������ۣ�
������P���߶�CD��ʱ����ͼ3��
��CP=2DP��CD=8��
��CP=![]() CD=
CD=![]() ��8=
��8=![]() ��
��
���P������3��![]() ����
����
������P���߶�CD���ӳ�����ʱ����ͼ4��
��CP=2DP��
��DP=CD=8��
���P������3��16����
������������P������3��![]() ����3��16��.
����3��16��.


ͼ3 ͼ4

����Ŀ��ij��������һ����Ʒ���ɱ�ÿǧ��40Ԫ���涨ÿǧ���ۼ۲����ڳɱ����Ҳ�����80Ԫ�����г����飬ÿ���������y��ǧ�ˣ���ÿǧ���ۼ�x��Ԫ������һ�κ�����ϵ�������������±���
�ۼ�x��Ԫ/ǧ�ˣ� | 50 | 60 | 70 |
������y��ǧ�ˣ� | 100 | 80 | 60 |
��1����y��x֮��ĺ�������ʽ��
��2������Ʒÿ���������ΪW��Ԫ�������ۼ�x��Ϊ����Ԫʱ������ÿ���ܻ�����������������Ƕ��٣�
��3���������Ҫ���ÿ�첻����1350Ԫ�������ҷ��ϳ����Լ��Ĺ涨����ô����Ʒÿǧ���ۼ۵�ȡֵ��Χ�Ƕ��٣���˵�����ɣ�
����Ŀ�������е��ش���̩������ⷿ������½���������ƻ�10���ڽ����������Ⱥ��ס�����⣬ǰ6�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=![]() x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-
x+5����x��λ���꣬1��x��6��xΪ����������4�꣬ÿ�꿢��Ͷ��ʹ�õĹ��ⷿ���y����λ������ƽ���ף�����ʱ��x�Ĺ�ϵ��y=-![]() x+
x+![]() ��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
��x��λ���꣬7��x��10��xΪ������������ÿ��Ĺ��ⷿȫ�������꣮���⣬����������ǵ����ص�Ӱ�죬ÿ������Ҳ��֮�ϵ���Ԥ�ƣ���x��Ͷ��ʹ�õĹ��ⷿ�����z����λ��Ԫ/m2����ʱ��x����λ���꣬1��x��10��xΪ����������һ�κ�����ϵ���±���
z��Ԫ/m2�� | 50 | 52 | 54 | 56 | 58 | �� |
x���꣩ | 1 | 2 | 3 | 4 | 5 | �� |
��1�����z��x�ĺ�����ϵʽ��
��2���������ڵڼ���Ͷ��Ĺ��ⷿ��ȡ�������࣬���Ϊ���ٰ���Ԫ��
��3������6�꿢��Ͷ��ʹ�õĹ��ⷿ�ɽ��20���˵�ס�����⣬�����ƻ��ڵ�10��Ͷ��Ĺ��ⷿ��������������£�Ҫ���˾�ס������ȵ�6���˾�ס��������a%�������ɽ��ס�����������ȵ�6�����1.35a%����a��ֵ��
���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��
����Ŀ�����չ�˾�������ֵĻ�������Ϊa(��λ��Ԫ)��������������ֵ�Ͷ���˳�Ϊ�����ˣ������˱���ȵı�����������ȳ��մ����Ĺ������±���
����ȳ��մ��� | 0 | 1 | 2 | 3 | 4 | ��5 |
���� | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
�ù�˾��������˸����ֵ�300����������һ���ڵij���������õ�����ͳ��ͼ��

(1)�����У����Ѹ��ڻ������ѵ�����Ϊ__________����
(2)��֪�����ֵĻ�������aΪ6 000Ԫ������1�������˱���ȵ�ƽ�����ѣ�