Question

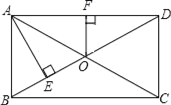
【题目】如图，在矩形ABCD中，对角线AC、BD交于点O， 自点A作AE⊥BD于点E，且BE：ED=1：3，过点O作OF⊥AD于点F，若OF=3cm，则BD的长为（　　）cm．

A.6B.9C.12D.15

Answer 1

【答案】C

【解析】

根据矩形的性质得出AC=BD，BD=2BO=2OD，AC=2AO，∠BAD=90°，求出AO=BO，根据等边三角形的判定得出△ABO是等边三角形，求出∠BAO=60°，∠DAO=30°，即可求出AO，即可求出答案．

∵四边形ABCD是矩形，∴AC=BD，BD=2BO=2OD，AC=2AO，∠BAD=90°，∴AO=BO，

∵BE：ED=1：3，∴BE=EO，

∵AE⊥BD，∴AB=AO，即AO=OB=AB，

∴△ABO是等边三角形，

∴∠BAO=60°，∴∠DAO=90°-60°=30°，

∵OF⊥AD于点F，OF=3cm，∴∠AFO=90°，AO=2OF=6cm，

∴AC=2AO=12cm，∴BD=12cm，故选C．