��Ŀ����
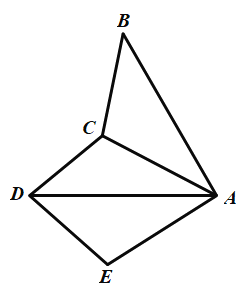
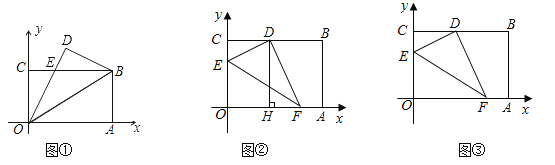
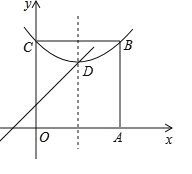
����Ŀ���Ķ�������Լ��,��ƽ��ֱ������ϵ��,����ij����ƽ�����������ƽ������������н�ƽ���ߵ�ֱ��,�иõ������������.����,��M(1��3)���������У�x=1��y=3��y=x+2��y=x+4.��ͼ,��ƽ��ֱ������ϵ����������OABC,��B�ڵ�һ����,A��C�ֱ���x���y����,������![]() ����B.C���㣬����D���������ڲ�.
����B.C���㣬����D���������ڲ�.
(1)���M��2,3����������������___________________
(2)����D��һ����������y=x+1����������ߵĽ���ʽ________________________
���𰸡�![]()
![]()
��������
��1������������ֱ�������D�������ߣ�
��2���ɵ�D��һ�������ߺ������ε����������D�����꣬�Ӷ���������߽���ʽ��
��1���ߵ�M��2��3����
���M��2��3����x=2��y=3��y=x+1��y=-x+5��
�ʴ�Ϊy=3��y=x+1��(2)��D��һ����������y=x+1����b-a=1����b=a+1
�������߽���ʽΪ![]()
��![]()
���ı���OABC�������Σ���D��Ϊ�����εĶԳ��ᣬD(a��b)��
��B(2a��2b)��
��![]() ����b=a+1����õ�a=2��b=3��
����b=a+1����õ�a=2��b=3��
��D(2��3)��
�������߽���ʽΪ![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ