题目内容
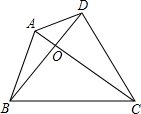
四边形ABCD是任意四边形,AC与BD交点O.求证:AC+BD>
(AB+BC+CD+DA).
证明:在△OAB中有OA+OB>AB
在△OAD中有______,
在△ODC中有______,
在△______中有______,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA
即:______,
即:AC+BD>
(AB+BC+CD+DA)
| 1 |
| 2 |
证明:在△OAB中有OA+OB>AB
在△OAD中有______,
在△ODC中有______,
在△______中有______,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA
即:______,
即:AC+BD>
| 1 |
| 2 |

证明:∵在△OAB中OA+OB>AB
在△OAD中有OA+OD>AD,
在△ODC中有OD+OC>CD,
在△OBC中有OB+OC>BC,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA
即2(AC+BD)>AB+BC+CD+DA,
即AC+BD>
(AB+BC+CD+DA).
故答案为:OA+OD>AD;OD-OC>CD;OBC;OB+OC>BC;2(AC+BD)>AB+BC+CD+DA.
在△OAD中有OA+OD>AD,
在△ODC中有OD+OC>CD,
在△OBC中有OB+OC>BC,
∴OA+OB+OA+OD+OD+OC+OC+OB>AB+BC+CD+DA
即2(AC+BD)>AB+BC+CD+DA,
即AC+BD>
| 1 |
| 2 |
故答案为:OA+OD>AD;OD-OC>CD;OBC;OB+OC>BC;2(AC+BD)>AB+BC+CD+DA.

练习册系列答案
相关题目