题目内容
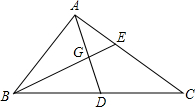
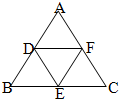
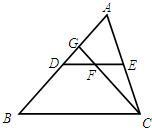
如图DE是△ABC的中位线，F是DE的中点，CF的延长线交AB于点G，则AG：GD等于（ ）
| A．2：1 | B．3：1 | C．3：2 | D．4：3 |
过E作EM∥AB与GC交于点M，
∴△EMF≌△DGF，
∴EM=GD，
∵DE是中位线，
∴CE=
AC，
又∵EM∥AG，
∴△CME∽△CGA，
∴EM：AG=CE：AC=1：2，
又∵EM=GD，
∴AG：GD=2：1．
故选A．
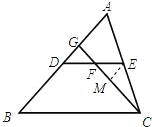
∴△EMF≌△DGF，
∴EM=GD，
∵DE是中位线，
∴CE=
| 1 |
| 2 |
又∵EM∥AG，
∴△CME∽△CGA，
∴EM：AG=CE：AC=1：2，
又∵EM=GD，
∴AG：GD=2：1．
故选A．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
