Question

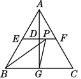
【题目】如图所示，在边长为2的等边三角形ABC中，G为BC的中点，D为AG的中点，过点D作EF∥BC交AB于E，交AC于F，P是线段EF上一个动点，连接BP，GP，则△BPG的周长的最小值是________．

Answer 1

【答案】3

【解析】

由于点G关于直线EF的对称点是A，所以当B、P、A三点在同一直线上时，BP+PG的值最小,此时△BPG的周长的最小．

解：由题意得AG⊥BC，点G与点A关于直线EF对称，

连接PA，则BP＋PG＝BP＋PA，

所以当点A，B，P在一条直线上时，BP＋PA的值最小，最小值为2.

由题可得BG＝1，

因为△BPG的周长为BG＋PG＋BP，

所以当BP＋PA的值最小时，△BPG的周长最小，最小值是3.

故答案为:3.