题目内容
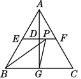
【题目】如图，直角三角板ABC的斜边AB＝12 cm，∠A＝30°，将三角板ABC绕点C顺时针旋转90°至三角板A′B′C′的位置后，再沿CB方向向左平移，使点B′落在原三角板ABC的斜边AB上，则三角板A′B′C′平移的距离为( )
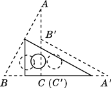
A. 6 cm B. 4 cm
C. (6－2
)cm D. (4－6)cm
【答案】C
【解析】
根据直角三角形30°角所对的直角边等于斜边的一半求出BC，再利用勾股定理列式求出AC，然后求出AB′，过点B′作B′D⊥AC交AB于D，然后解直角三角形求出B′D即可．
解：
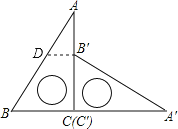
∵AB=12cm，∠A=30°，
∴BC=
AB=×12=6cm，
由勾股定理得，AC=
=
=6
cm，
∵三角板ABC绕点C顺时针旋转90°得到三角板A′B′C′，
∴B′C′=BC=6cm，
∴AB′=AC-B′C′=6-6，
过点B′作B′D⊥AC交AB于D，
则B′D=
AB′=×（6-6）=（6-2）cm．
故选：C．
练习册系列答案
相关题目
【题目】某产品每件的成本为10元，在试销阶段每件产品的日销售价x（元）与产品的日销售量y（件）之间的关系如下表：
X（元） | 15 | 20 | 25 | … |
Y（件） | 25 | 20 | 15 | … |
（1）观察与猜想y与x的函数关系，并说明理由．
（2）求日销售价定为30元时每日的销售利润．
【题目】某兴趣小组10名学生在一次数学测试中的成绩如表（满分150分）
分数（单位：分） | 105 | 130 | 140 | 150 |
人数（单位：人） | 2 | 4 | 3 | 1 |
下列说法中，不正确的是（ ）
A.这组数据的众数是130
B.这组数据的中位数是130
C.这组数据的平均数是130
D.这组数据的方差是112.5
