题目内容
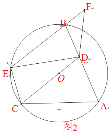
【题目】矩形ABCD中,对角线AC、BD交于点O,AE⊥BD于E,∠CAE=10°,则∠ADB=_____.
【答案】50°或40°
【解析】
分两种情况,求出∠AOD=80°,由矩形的性质得出OA=OD,由等腰三角形的性质和矩形的性质即可得出答案.
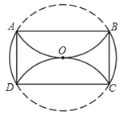
解:①AB>AD时,如图1所示:
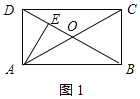
∵AE⊥BD,
∴∠AOD=90°﹣∠CAE=90°﹣10°=80°,
∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC=![]() AC,OB=OD=
AC,OB=OD=![]() BD,AC=BD,
BD,AC=BD,
∴OA=OD,
∴∠ADB=∠OAD=![]() (180°﹣80°)=50°;
(180°﹣80°)=50°;
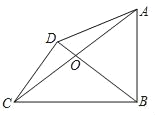
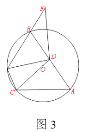
②AD>AB时,如图2所示:
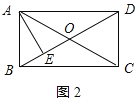
同①得:OA=OB,
∴∠ABD=∠OAB=![]() (180°﹣80°)=50°,
(180°﹣80°)=50°,
∴∠ADB=90°﹣∠ABD=40°;
综上所述,∠ADB=50°或40°;
故答案为:50°或40°.

练习册系列答案
相关题目