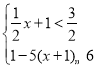ƒøƒ⁄»ð
°æƒø°ø◊€∫œ”ÎÃΩæø£Æ
»ÁÕº1£¨≈◊ŒÔœþy£Ω![]() x2©Å
x2©Å![]() x©Å2”Îx÷·Ωª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨æ≠π˝µ„Bµƒ÷±œþΩªy÷·”⁄µ„E£®0£¨2£©£Æ
x©Å2”Îx÷·Ωª”⁄A£¨B¡Ωµ„£¨”Îy÷·Ωª”⁄µ„C£¨æ≠π˝µ„Bµƒ÷±œþΩªy÷·”⁄µ„E£®0£¨2£©£Æ
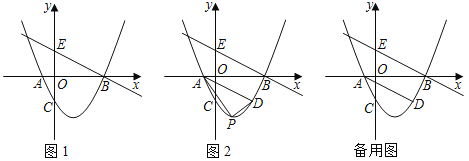
£®1£©«ÛA£¨B£¨C»˝µ„µƒ◊¯±Íº∞÷±œþBEµƒΩ‚Œˆ Ω£Æ
£®2£©»ÁÕº2£¨π˝µ„A◊˜BEµƒ∆Ω––œþΩª≈◊ŒÔœþ”⁄µ„D£¨µ„P «≈◊ŒÔœþ…œŒª”⁄œþ∂ŒADœ¬∑Ωµƒ“ª∏ˆ∂ص„£¨¡¨Ω”PA£¨PD£¨«ÛOAPD√ʪ˝µƒ◊Ó¥Û÷µ£Æ
£®3£©»Ù£®2£©÷–µƒµ„PŒ™≈◊ŒÔœþ…œ“ª∂ص„£¨‘⁄x÷·…œ «∑ҥʑ⁄µ„Q£¨ πµ√“‘A£¨D£¨P£¨QŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£ø»Ù¥Ê‘⁄£¨«Î÷±Ω”–¥≥ˆµ„Qµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø(1)A£®©Å1£¨0£©£¨B£®4£¨0£©£¨C£®0£¨©Å2£©£ªy£Ω©Å![]() x+2£ª(2) 4£ª(3)¥Ê‘⁄£ªµ„Qµƒ◊¯±ÍŒ™£®2£¨0£©ªÚ£®©Å4£¨0£©ªÚ£®
x+2£ª(2) 4£ª(3)¥Ê‘⁄£ªµ„Qµƒ◊¯±ÍŒ™£®2£¨0£©ªÚ£®©Å4£¨0£©ªÚ£®![]() £¨0£©ªÚ£®
£¨0£©ªÚ£®![]() £¨0£©£Æ
£¨0£©£Æ
°æΩ‚Œˆ°ø
£®1£©¡Óy=0ø…«ÛA”ÎBµ„◊¯±Í£¨¡Óx=0ø…«Û≥ˆCµ„µƒ◊¯±Í£ª…Ë÷±œþBEµƒΩ‚Œˆ ΩŒ™y=kx+b£¨Ω´B£®4£¨0£©°¢E£®0£¨2£©¥˙»ÎΩ‚Œˆ Ωø…«Ûk”Îbµƒ÷µ£ª
£®2£©…ËADµƒΩ‚Œˆ ΩŒ™y=-![]() x+m£¨Ω´A£®-1£¨0£©¥˙»Î«Û≥ˆm£¨Ω¯∂¯»∑∂®÷±œþADµƒΩ‚Œˆ Ω£¨‘Ÿ¡™¡¢
x+m£¨Ω´A£®-1£¨0£©¥˙»Î«Û≥ˆm£¨Ω¯∂¯»∑∂®÷±œþADµƒΩ‚Œˆ Ω£¨‘Ÿ¡™¡¢ «Û≥ˆDµ„◊¯±Í£¨π˝µ„P◊˜PF°Õx÷·”⁄µ„F£¨ΩªAD”⁄µ„N£¨π˝µ„D◊˜DG°Õx÷·”⁄µ„G£Æ‘ÚS°˜APD=S°˜APN+S°˜DPN=2PN£¨…ËP
«Û≥ˆDµ„◊¯±Í£¨π˝µ„P◊˜PF°Õx÷·”⁄µ„F£¨ΩªAD”⁄µ„N£¨π˝µ„D◊˜DG°Õx÷·”⁄µ„G£Æ‘ÚS°˜APD=S°˜APN+S°˜DPN=2PN£¨…ËP![]() £¨‘ÚN
£¨‘ÚN![]() £¨«Û≥ˆPN=-
£¨«Û≥ˆPN=-![]() a2+a+
a2+a+![]() £¨À˘“‘S°˜APD=-a2+2a+3=-£®a-1£©2+4£¨µ±a=1 ±£¨°˜APDµƒ√ʪ˝◊Ó¥Û£¨◊Ó¥Û÷µŒ™4£ª
£¨À˘“‘S°˜APD=-a2+2a+3=-£®a-1£©2+4£¨µ±a=1 ±£¨°˜APDµƒ√ʪ˝◊Ó¥Û£¨◊Ó¥Û÷µŒ™4£ª
£®3£©∑÷¡Ω÷÷«ÈøˆÃ÷¬€£∫¢Ÿµ±PD”ÎAQŒ™∆Ω––Àƒ±þ–Œµƒ∂‘±þ ±£¨”…PD=AQ=3£¨ø…«ÛQ£®2£¨0£©ªÚQ£®-4£¨0£©£ª¢⁄µ±PD”ÎAQŒ™∆Ω––Àƒ±þ–Œµƒ∂‘Ω«œþ ±£¨œ»«Û≥ˆP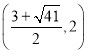 ªÚP
ªÚP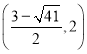 £¨‘Ÿ«Û≥ˆPDµƒ÷–µ„Œ™
£¨‘Ÿ«Û≥ˆPDµƒ÷–µ„Œ™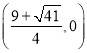 ªÚ
ªÚ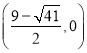 £¨”…∆Ω––Àƒ±þ–Œ∂‘Ω«œþµƒ–‘÷ ø…«ÛQ
£¨”…∆Ω––Àƒ±þ–Œ∂‘Ω«œþµƒ–‘÷ ø…«ÛQ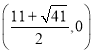 ªÚQ
ªÚQ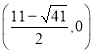 £Æ
£Æ
Ω‚£∫£®1£©¡Óy£Ω0£¨‘Ú![]() x2©Å
x2©Å![]() x©Å2£Ω0£¨Ω‚µ√x£Ω4ªÚx£Ω©Å1£¨
x©Å2£Ω0£¨Ω‚µ√x£Ω4ªÚx£Ω©Å1£¨
°ýA£®©Å1£¨0£©£¨B£®4£¨0£©£¨
¡Óx£Ω0£¨‘Úy£Ω©Å2£¨°ýC£®0£¨©Å2£©£¨
…Ë÷±œþBEµƒΩ‚Œˆ ΩŒ™y£Ωkx+b£¨
Ω´B£®4£¨0£©°¢E£®0£¨2£©¥˙»Îµ√£¨![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫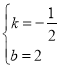 £¨
£¨
°ýy£Ω©Å![]() x+2£ª
x+2£ª
£®2£©”…“‚ø……ËADµƒΩ‚Œˆ ΩŒ™y£Ω©Å![]() x+m£¨
x+m£¨
Ω´A£®©Å1£¨0£©¥˙»Î£¨µ√µΩm£Ω©Å![]() £¨
£¨
°ýy£Ω©Å![]() x©Å
x©Å![]() £¨
£¨
¡™¡¢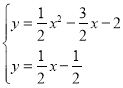 £¨
£¨
Ω‚µ√£∫![]() £¨
£¨![]() £¨
£¨
°ýD£®3£¨©Å2£©£¨
π˝µ„P◊˜PF°Õx÷·”⁄µ„F£¨ΩªAD”⁄µ„N£¨π˝µ„D◊˜DG°Õx÷·”⁄µ„G£Æ
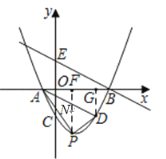
°ýS°˜APD£ΩS°˜APN+S°˜DPN£Ω![]() PNAF+
PNAF+![]() PNFG£Ω
PNFG£Ω![]() PN£®AF+FG£©£Ω
PN£®AF+FG£©£Ω![]() PNAG£Ω
PNAG£Ω![]() °¡4PN£Ω2PN£¨
°¡4PN£Ω2PN£¨
…ËP£®a£¨©Å![]() a2©Å
a2©Å![]() a©Å2£©£¨‘ÚN£®a£¨©Å
a©Å2£©£¨‘ÚN£®a£¨©Å![]() a©Å
a©Å![]() £©£¨
£©£¨
°ýPN£Ω©Å![]() a2+a+
a2+a+![]() £¨
£¨
°ýS°˜APD£Ω©Åa2+2a+3£Ω©Å£®a©Å1£©2+4£¨
°þ©Å1£º0£¨©Å1£ºa£º3£¨
°ýµ±a£Ω1 ±£¨°˜APDµƒ√ʪ˝◊Ó¥Û£¨◊Ó¥Û÷µŒ™4£ª
£®3£©¥Ê‘⁄£ª
¢Ÿµ±PD”ÎAQŒ™∆Ω––Àƒ±þ–Œµƒ∂‘±þ ±£¨
°þAQ°ŒPD£¨AQ‘⁄x÷·…œ£¨
°ýP£®0£¨©Å2£©£¨
°ýPD£Ω3£¨
°ýAQ£Ω3£¨
°þA£®©Å1£¨0£©£¨
°ýQ£®2£¨0£©ªÚQ£®©Å4£¨0£©£ª
¢⁄µ±PD”ÎAQŒ™∆Ω––Àƒ±þ–Œµƒ∂‘Ω«œþ ±£¨
PD”ÎAQµƒ÷–µ„‘⁄x÷·…œ£¨
°ýPµ„µƒ◊ð◊¯±ÍŒ™2£¨
°ýP£®![]() £¨2£©ªÚP£®
£¨2£©ªÚP£®![]() £¨2£©£¨
£¨2£©£¨
°ýPDµƒ÷–µ„Œ™£®![]() £¨0£©ªÚ£®
£¨0£©ªÚ£®![]() £¨0£©£¨
£¨0£©£¨
°þQµ„”ÎAµ„πÿ”⁄PDµƒ÷–µ„∂‘≥∆£¨
°ýQ£®![]() £¨0£©ªÚQ£®
£¨0£©ªÚQ£®![]() £¨0£©£ª
£¨0£©£ª
◊€…œÀ˘ ˆ£∫µ„Qµƒ◊¯±ÍŒ™£®2£¨0£©ªÚ£®©Å4£¨0£©ªÚ£®![]() £¨0£©ªÚ£®
£¨0£©ªÚ£®![]() £¨0£©£Æ
£¨0£©£Æ

 »´ƒÐ≤‚øÿ∆⁄ƒ©–°◊¥‘™œµ¡–¥∞∏
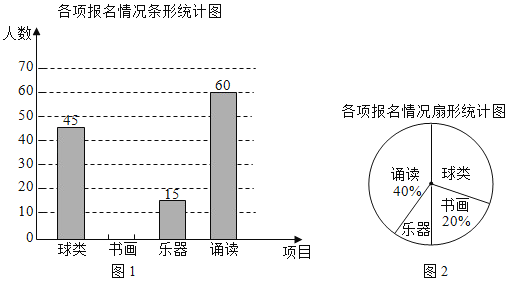
»´ƒÐ≤‚øÿ∆⁄ƒ©–°◊¥‘™œµ¡–¥∞∏°æƒø°ø °∞¡˘“ª°±«∞œ¶÷ ºý≤ø√≈¥”ƒ≥≥¨ –æ≠œ˙µƒ∂˘ÕØÕÊæþ°¢ÕØ≥µ∫ÕÕØ◊∞÷–π≤≥È≤È¡À300º˛∂˘ÕØ”√∆∑£¨“‘œ¬ «∏˘æð≥È≤ÈΩ·π˚ªÊ÷∆≥ˆµƒ≤ªÕÍ’˚µƒÕ≥º∆±Ì∫Õ…»–ŒÕº£ª
¿ý± | ∂˘ÕØÕÊæþ | ÕØ≥µ | ÕØ◊∞ |
≥È≤Ⱥ˛ ˝ | 90 |

«Î∏˘æð…œ ˆÕ≥º∆±Ì∫Õ…»–ŒÃ·π©µƒ–≈œ¢£¨ÕÍ≥…œ¬¡–Œ £∫
£®1£©∑÷±≤π»´…œ ˆÕ≥º∆±Ì∫ÕÕ≥º∆Õº£ª
£®2£©“—÷™À˘≥È≤ȵƒ∂˘ÕØÕÊæþ°¢ÕØ≥µ°¢ÕØ◊∞µƒ∫œ∏Ò¬ ∑÷±Œ™90%°¢88%°¢80%£¨»Ù¥”∏√≥¨ –µƒ’‚»˝¿ý∂˘ÕØ”√∆∑÷–Àʪ˙π∫¬Ú“ªº˛£¨¬ÚµΩ∫œ∏Ò∆∑µƒ∏≈¬ «∂ý…Ÿ£ø