Question

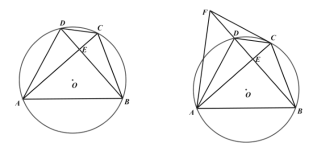
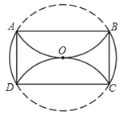
【题目】如图，在⊙O中，分别将弧AB、弧CD沿两条互相平行的弦AB、CD折叠，折叠后的弧均过圆心，若⊙O的半径为4，则四边形ABCD的面积是__________________．

Answer 1

【答案】

【解析】

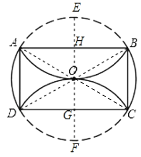
作OH⊥AB，延长OH交于E，反向延长OH交CD于G，交于F，连接OA、OB、OC、OD，根据折叠的对称性及三角形全等，证明AB=CD，又因AB∥CD，所以四边形ABCD是平行四边形，由平行四边形面积公式即可得解．

如图，作OH⊥AB，垂足为H，延长OH交于E，反向延长OH交CD于G，交于F，连接OA、OB、OC、OD，则OA=OB=OC=OD=OE=OF=4，

∵弧AB、弧CD沿两条互相平行的弦AB、CD折叠，折叠后的弧均过圆心，

∴OH=HE=，OG=GF=，即OH=OG，

又∵OB=OD，

∴Rt△OHB≌Rt△OGD，

∴HB=GD，

同理，可得AH=CG= HB=GD

∴AB=CD

又∵AB∥CD

∴四边形ABCD是平行四边形，

在Rt△OHA中，由勾股定理得：

AH=

∴AB=

∴四边形ABCD的面积=AB×GH=．

故答案为： ．