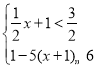题目内容
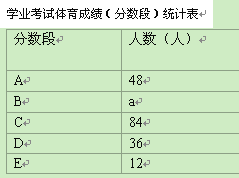
【题目】某企业拥有一条生产某品牌酸奶的生产线，已知该酸奶销售额为4800元时的销量比销售额为800元时的销量要多500瓶．现接到一单生产任务，需要在16天内完成，为按时完成任务，该企业招收了新工人甲，设甲第x天（x为整数）生产的酸奶数量为y瓶，y与x满足下列关系式：y＝
．
（1）求每瓶酸奶的售价为多少元？
（2）如图，设第x天每瓶酸奶的成本是p元，已知p与x之间的关系可以用图中的函数图象来刻画．若甲第x天创造的利润为w元，请直接写出w与x之间的函数表达式，并求出第几天的利润最大，最大利润是多少元？（利润＝售价﹣成本）
（3）设（2）小题中第m天利润达到最大值，若要使第（m+1）天的利润比第m天的利润至少多50元，则第（m+1）天每瓶酸奶至少应提价几元？
【答案】（1）每瓶酸奶的售价为8元；（2）w＝﹣10（x﹣10）2+1960，第10天的利润最大，最大利润是1960元；（3）第（m+1）天每瓶酸奶至少应提价0.1元
【解析】
（1）根据“销售额为4800元时的销量比销售额为800元时的销量要多500瓶”列出分式方程即可求得；
（2）根据图象求得成本p与x之间的关系，然后根据利润等于订购价减去成本价，然后整理即可得到w与x的关系式，再根据一次函数的增减性和二次函数的增减性解答；
（3）根据（2）得出m+1＝11，根据利润等于订购价减去成本价得出提价a与利润w的关系式，再根据题意列出不等式求解即可．
解：（1）设售价为x元，
根据题意得：
，
解得：x＝8，
经检验：x＝8是原方程的根，
答：每瓶酸奶的售价为8元；
（2）由图象得，当0≤x≤8时，p＝4；
当8≤x≤16时，设p＝kx+b，
把点（8，4），（16，6）代入得，
，
解得：
，
∴p＝
x+2，
当0≤x≤8时，w＝（8﹣4）×50x＝200x，
此时当x＝8时，w取得最大值1600；
当8≤x≤16时，
w＝（8﹣x﹣2）×（40x+160）
＝﹣10x2+200x+960
＝﹣10（x﹣10）2+1960，
所以当x＝10时，w取得最大值1960；
综上，第10天的利润最大，最大利润是1960元；
（3）由（2）可知m＝10，m+1＝11，
设第11天提价a元，
由题意得，w11＝（8+a﹣p）（40x+160）＝600（a+3.25），
∴600（a+3.25）﹣1960≥50，
解得：a≥0.1，
答：第（m+1）天每瓶酸奶至少应提价0.1元．
