题目内容
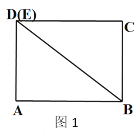
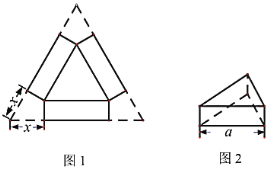
【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
【答案】(1)(1)![]() ,
,![]() ;(2)①表格见解析;②描点见解析;③连线见解析;(3)①4;②
;(2)①表格见解析;②描点见解析;③连线见解析;(3)①4;②![]() .
.
【解析】
(1)根据正三棱柱的体积公式可以列出y关于x的函数表达式,根据x的实际意义可直接分析出其取值范围;
(2)①分别将x=1和2代入函数关系式可求出y的值;②根据表内数据可在平面直角坐标系上描点;③可直接用平滑曲线连接;
(3)根据图象即可得到结论.
解:(1)∵无盖糖果盒的高为![]() ,a=6-2x,
,a=6-2x,
∴底面正三角形的面积为![]() ,
,
![]() ,
,
故答案为:y=x(3-x)2,0<x<3;
(2)①列表:补充表格中的数据;
x | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
y | 4 | 2 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;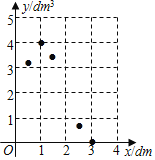
③连线:用光滑的曲线顺次连接各点.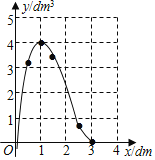
(3)①该糖果盒的最大容积是4;
②由图象可知:0.27<x<2,
因为a=6-2x,
所以2<a<5.5.
故答案为:4;2<a<5.5.
【点晴】
本题考查了二次函数的应用,函数的性质,画函数图象的步骤列表、描点、连线,以及数形结合思想的运用等,解题关键是要熟练掌握函数的定义及数形结合的思想.

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案