题目内容
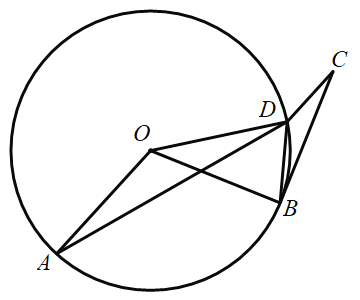
【题目】如图,数轴上![]() 三个数所对应的点分别为
三个数所对应的点分别为![]() ,已知
,已知![]() ,且
,且![]() 的倒数是它本身,且
的倒数是它本身,且![]() 满足
满足![]() .
.
![]()
(1)求代数式![]() 的值:
的值:
(2)若将数轴折叠,使得点![]() 与点
与点![]() 重合,则与点
重合,则与点![]() 重合的点表示的数是_______;
重合的点表示的数是_______;
(3)请在数轴上确定一点![]() ,使得
,使得![]() ,则点
,则点![]() 表示的数是______.
表示的数是______.
【答案】(1)64;(2)-7;(3)4或-8.
【解析】
(1)根据平方和绝对值的非负性即可求出a和c,然后代入求值即可;
(2)根据题意,求出b的值,然后求出线段AB的中点,即可求出结论;
(3)设点![]() 表示的数为
表示的数为![]() ,然后根据点D和点A的位置关系分类讨论,分别根据
,然后根据点D和点A的位置关系分类讨论,分别根据![]() 列出方程即可分别求出结论.
列出方程即可分别求出结论.
解:(1)∵![]() ,
,
∴![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() ;
;
(2)∵![]() ,且
,且![]() 的倒数是它本身,
的倒数是它本身,
∴![]() ,
,
∴线段AB的中点为![]() ,
,
∴![]() ,
,![]() ,
,
∴与点![]() 重合的点表示的数是
重合的点表示的数是![]() ;
;
故答案为:![]() ;
;
(3)设点![]() 表示的数为
表示的数为![]() ,
,
若点![]() 在点
在点![]() 的左侧,
的左侧,
∵![]()
则![]() ,
,
解得![]() ;
;
若点![]() 在点
在点![]() 的右侧,
的右侧,
∵![]()
则![]() ,
,
解得![]() ;
;
综上所述,点![]() 表示的数是4或-8.
表示的数是4或-8.
故答案为:4或-8.

 寒假学与练系列答案
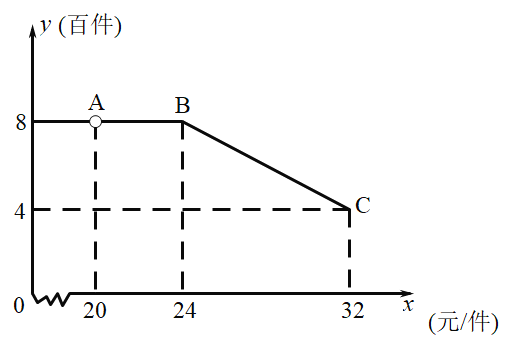
寒假学与练系列答案【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇,下表是该型号电风扇近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
![]() 求A、B两种型号的电风扇的销售单价;
求A、B两种型号的电风扇的销售单价;
![]() 若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台,假设售价不变,那么商场应采用哪种采购方案,才能使得当销售完这些风扇后,商场获利最多?最多可获利多少元?
【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
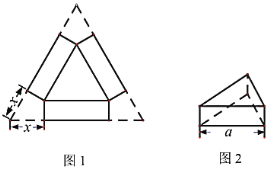
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)
【题目】为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为![]() 分)、
分)、![]() 分)、
分)、![]() 分)、
分)、![]() 分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
分)四个等级进行统计,并将统计结果绘制成如下统计图表,请你根据统计图解答以下问题:
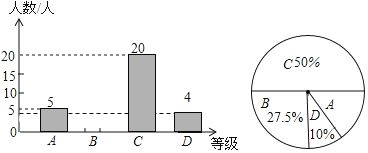
其中组![]() 的期末数学成绩如下
的期末数学成绩如下
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请补全条形统计图;
(2)这部分学生的期末数学成绩的中位数是 ,![]() 组的期末数学成绩的众数是 ;
组的期末数学成绩的众数是 ;
(3)这个学校九年级共有学生![]() 人,若分数为
人,若分数为![]() 分(含
分(含![]() 分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?
分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?