题目内容
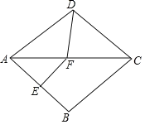
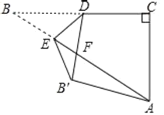
【题目】如图,在Rt△ABC中,∠C=90°,BC=4![]() ,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
,AC=4,点D是BC的中点,点E是边AB上一动点,沿DE所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若∠AB′F为直角,则AE的长为__________.
【答案】![]()
【解析】
作EH⊥AB′交AB′的延长线于H.设AE=x.证明Rt△ADC≌Rt△ADB′(HL),得出AC=AB′=4,在Rt△EHB′中,B′H=![]() B′E=
B′E=![]() (8-x),EH=
(8-x),EH=![]() B′H=
B′H=
![]() (8-x),在Rt△AEH中,由勾股定理得出方程,解方程即可.
(8-x),在Rt△AEH中,由勾股定理得出方程,解方程即可.
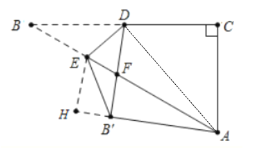
解:作EH⊥AB′交AB′的延长线于H,连接AD.设AE=x.
在Rt△ABC中,,BC=4![]() ,AC=4,∴AB=8,tanB=
,AC=4,∴AB=8,tanB=![]() =
=![]()
∴∠B=30°.
∵点D是BC的中点,∴BD=DC
由折叠的性质,得BD= DB′.
∴CD=DB′,
∵AD=AD,
∴Rt△ADC≌Rt△ADB′(HL),
∴AC=AB′=4,
∵∠AB′E=∠AB′F+∠EB′F=90°+30°=120°,
∴∠EB′H=60°,
在Rt△EHB′中,B′H=![]() B′E=
B′E=![]() (8-x),EH=
(8-x),EH=![]() B′H
B′H
![]() (8-x),
(8-x),
在Rt△AEH中,∵EH2+AH2=AE2,
∴[![]() (8-x)]2+[4+
(8-x)]2+[4+![]() (8-x)]2=x2,
(8-x)]2=x2,
解得:x=![]() .
.

 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
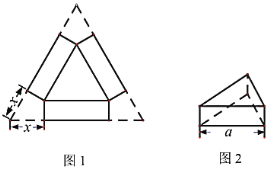
小学能力测试卷系列答案【题目】如图1,小明用一张边长为![]() 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒,从三个角处分别剪去一个形状大小相同的四边形,其一边长记为![]() ,再折成如图2所示的无盖糖果盒,它的容积记为
,再折成如图2所示的无盖糖果盒,它的容积记为![]() .
.
(1)![]() 关于
关于![]() 的函数关系式是__________,自变量
的函数关系式是__________,自变量![]() 的取值范围是__________.
的取值范围是__________.
(2)为探究![]() 随
随![]() 的变化规律,小明类比二次函数进行了如下探究:
的变化规律,小明类比二次函数进行了如下探究:
①列表:请你补充表格中的数据:
| 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
| 0 | 3.125 | ________ | 3.375 | ________ | 0.625 | 0 |
②描点:请你把上表中各组对应值作为点的坐标,在平面直角坐标系中描出相应的点;
③连线:请你用光滑的曲线顺次连接各点.

(3)利用函数图象解决:
①该糖果盒的最大容积是__________;
②若该糖果盒的容积超过![]() ,请估计糖果盒的底边长
,请估计糖果盒的底边长![]() 的取值范围.(保留一位小数)
的取值范围.(保留一位小数)