题目内容
【题目】如图，将一张矩形纸片ABCD沿着对角线BD向上折叠，顶点C落到点E处，BE交AD于点F．
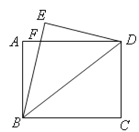
（1）求证：△BDF是等腰三角形；
（2）若AB=6，AD=8，求AF的长．
【答案】（1）见解析；（2）AF=
．
【解析】
（1）证明△BDF是等腰三角形，可证明BF=DF，可通过证明∠EBD=∠FDB实现，利用折叠的性质和平行线的性质解决；
（1）设AF=x，则BF=DF=8-x，在Rt△ABF中，利用勾股定理构造方程即可求解．
（1）根据折叠的性质可得∠DBC=∠DBE，
∵AD∥BC，
∴∠DBC=∠ADB，
∴∠DBE=∠ADB，
∴DF=BF，
∴△BDF是等腰三角形；
（2）设AF=x，则BF=DF=8-x，
在Rt△ABF中，AB2+AF2=BF2，即62+x2=(8﹣x)2，
解得x=，即AF=．
小学生10分钟口算测试100分系列答案
【题目】某电器商场销售每台进价分别为200元、170元的A、B两种型号的电风扇，下表是该型号电风扇近两周的销售情况：
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
求A、B两种型号的电风扇的销售单价；
若该商场准备用不多于5400元的金额再采购这两种型号的电风扇共30台，假设售价不变，那么商场应采用哪种采购方案，才能使得当销售完这些风扇后，商场获利最多？最多可获利多少元？
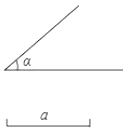
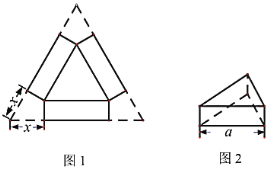
【题目】如图1，小明用一张边长为
的正三角形硬纸板设计一个无盖的正三棱柱糖果盒，从三个角处分别剪去一个形状大小相同的四边形，其一边长记为
，再折成如图2所示的无盖糖果盒，它的容积记为
．
（1）
关于
的函数关系式是__________，自变量的取值范围是__________．
（2）为探究随的变化规律，小明类比二次函数进行了如下探究：
①列表：请你补充表格中的数据：
| 0 | 0．5 | 1 | 1．5 | 2 | 2．5 | 3 |
| 0 | 3．125 | ________ | 3．375 | ________ | 0．625 | 0 |
②描点：请你把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；
③连线：请你用光滑的曲线顺次连接各点．
（3）利用函数图象解决：
①该糖果盒的最大容积是__________；
②若该糖果盒的容积超过
，请估计糖果盒的底边长
的取值范围．（保留一位小数）
