题目内容
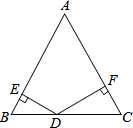
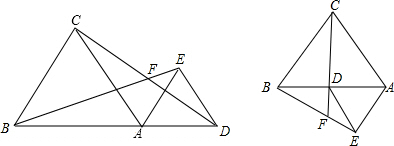
已知如下图所示,在等边△ABC和等边△ADE中,点B、A、D在一条直线上,BE、CD交于F.
(1)求证:△BAE≌△CAD.
(2)求∠BFC的大小.
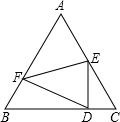
(3)在图1的基础上,将△ADE绕点A按顺时针方向旋转180°,此时BE交CD的延长线于点F,其他条件不变,得到图2所示的图形,请直接写出(1)、(2)中结论是否仍然成立.
(1)求证:△BAE≌△CAD.
(2)求∠BFC的大小.
(3)在图1的基础上,将△ADE绕点A按顺时针方向旋转180°,此时BE交CD的延长线于点F,其他条件不变,得到图2所示的图形,请直接写出(1)、(2)中结论是否仍然成立.

(1)证明:∵等边△ABC和等边△ADE,
∴AB=AC,AD=AE,∠CAB=∠EAD=60°,
∴∠CAE=60°,
∠BAE=∠CAD=120°,
∴△BAE≌△CAD,
(2)∵△BAE≌△CAD,
∴∠ADC=∠AEB,
∵∠BFC=∠ABE+∠ADC,
∴∠BFC=∠ABE+∠AEB,
∵∠ABE+∠AEB=180°-∠BAE,∠BAE=120°,
∴∠BFC=60°,
(3)成立.
∵等边△ABC和等边△ADE,
∴AE=AD,AC=AB,∠BAE=∠CAD=60°,
∴△BAE≌△CAD,
∵∠CDA=∠AEB,
∴∠ABE+∠BDF=∠ABE+∠CDA=∠ABE+∠AEB,
∵∠ABE+∠AEB=180°-∠BAE=180°-60°=120°,
∴∠ABE+∠BDF=120°,
∠BFC=180°-(∠ABE+∠BDF)=60°.
∴AB=AC,AD=AE,∠CAB=∠EAD=60°,
∴∠CAE=60°,
∠BAE=∠CAD=120°,
∴△BAE≌△CAD,
(2)∵△BAE≌△CAD,
∴∠ADC=∠AEB,
∵∠BFC=∠ABE+∠ADC,
∴∠BFC=∠ABE+∠AEB,
∵∠ABE+∠AEB=180°-∠BAE,∠BAE=120°,
∴∠BFC=60°,
(3)成立.
∵等边△ABC和等边△ADE,
∴AE=AD,AC=AB,∠BAE=∠CAD=60°,
∴△BAE≌△CAD,
∵∠CDA=∠AEB,
∴∠ABE+∠BDF=∠ABE+∠CDA=∠ABE+∠AEB,
∵∠ABE+∠AEB=180°-∠BAE=180°-60°=120°,
∴∠ABE+∠BDF=120°,
∠BFC=180°-(∠ABE+∠BDF)=60°.

练习册系列答案
相关题目