题目内容
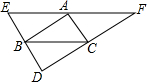如图，已知EF、ED、FD分别过△ABC的顶点A、B、C，且EF∥BC，ED∥AC，FD∥AB，求证：点A、B、C分别是线段EF、ED、DF的中点．考点：平行四边形的判定与性质
专题：证明题
分析：由EF∥BC，ED∥AC，FD∥AB，则可判定四边形ACBE，四边形ABDC，四边形ABCF是平行四边形，即可得AC=BE=BD，AB=CD=CF，BC=AE=AF，继而证得结论．
解答：证明：∵EF∥BC，ED∥AC，FD∥AB，
∴四边形ACBE，四边形ABDC，四边形ABCF是平行四边形，
∴AC=BE=BD，AB=CD=CF，BC=AE=AF，
∴点A、B、C分别是线段EF、ED、DF的中点．
∴四边形ACBE，四边形ABDC，四边形ABCF是平行四边形，
∴AC=BE=BD，AB=CD=CF，BC=AE=AF，
∴点A、B、C分别是线段EF、ED、DF的中点．
点评：此题考查了平行四边形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
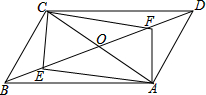如图，在平行四边形ABCD中，AC，BD相交于点O，AC=6，BD=8，∠AOD=65°，点E在BO上，AF∥CE交BD于点F．
一条公路弯道处是一段圆弧（弧AB），点O是这条弧所在圆的圆心，过点O作OC⊥AB，交弦AB于点D，交弧AB于点C，AB=120m，CD=20m，求这段弯道的半径OC的长．
已知一次函数y=kx+b的图象是直线l（如图），则不等式kx+b＞1的解集
如图，P是矩形ABCD的边AD上一个动点，矩形的两条边AB、BC的长分别为6和8，那么点P到矩形的两条对角线AC和BD的距离之和是