题目内容
在△ABC中,AB=AC=2,BD⊥AC,D为垂足,若∠ABD=30°,则BC长为 .
考点:含30度角的直角三角形,等腰三角形的性质,勾股定理
专题:计算题
分析:分为两种情况,画出图形,求出AD、CD的长,根据勾股定理求出BD,再根据勾股定理求出BC即可.
解答:解:分为两种情况:①
如图1,∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=
AB=1,
∴CD=2-1=1,
由勾股定理得:BD=
=
,
由勾股定理得:BC=
=
=2;
②如图2,∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=
AB=1,
∴CD=2+1=3,
由勾股定理得:BD=
=
,
由勾股定理得:BC=
=
=2
;
故答案为:2或2
.

如图1,∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=
| 1 |
| 2 |
∴CD=2-1=1,
由勾股定理得:BD=
| 22-12 |
| 3 |
由勾股定理得:BC=
| BD2+DC2 |
(
|
②如图2,∵BD⊥AC,
∴∠BDA=90°,
∵∠ABD=30°,AB=2,
∴AD=
| 1 |
| 2 |
∴CD=2+1=3,
由勾股定理得:BD=
| 22-12 |
| 3 |
由勾股定理得:BC=
| BD2+DC2 |
(
|
| 3 |
故答案为:2或2
| 3 |
点评:本题考查了含30度角的直角三角形性质和勾股定理,等腰三角形的性质的应用,注意:在直角三角形中,如果有一个角等于30°,那么它所对的直角边等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
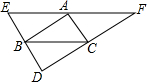 如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.
如图,已知EF、ED、FD分别过△ABC的顶点A、B、C,且EF∥BC,ED∥AC,FD∥AB,求证:点A、B、C分别是线段EF、ED、DF的中点.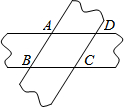 用两张平行的纸条交叉重叠放在一起,则四边形ABCD为
用两张平行的纸条交叉重叠放在一起,则四边形ABCD为 如图,在四边形ABCD中,AD∥BC,AD=15cm,BC=10cm,P、Q分别从A、C同时出发,P以3cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,运动
如图,在四边形ABCD中,AD∥BC,AD=15cm,BC=10cm,P、Q分别从A、C同时出发,P以3cm/s的速度由A向D运动,Q以2cm/s的速度由C出发向B运动,运动